3-15-11. George Howard Darwin to H. Poincaré
May 28.01
Newnham Grange–Cambridge
Dear Monsieur Poincaré,
I think it will interest you to hear that I have determined the limiting stability of the Jacobian ellipsoid.11 1 One of Poincaré’s major results concerning the stability of equilibrium figures is the proof of the fact, asserted but not rigorously proved by Lord Kelvin (1879, § 778" g), that beyond an upper limit of the angular momentum, Jacobian ellipsoids cease to be stable (Poincaré 1885, 373). Poincaré proved that there is an upper limit but gave no figures for the critical Jacobian ellipsoid (which is actually the first point of bifurcation of the series). Darwin gave numerical results concerning the bifurcation of the Jacobi series from the Maclaurin series as early as 1886 (Darwin 1886); these earlier numerical results are taken up in his later paper (Darwin 1902b, 326). Darwin cited Kelvin along with Poincaré’s Acta paper (Poincaré 1885), but addressed stability only briefly, without determining the limiting stability (Darwin 1886, 328). It occurs when . The axes of the ellipsoid are22 2 In the formula, denotes angular velocity (rotation around ) and the density of the body. In the final publication of these results, Darwin gives slightly different values (translated in the present notation): , , , (Darwin 1902b, 325). For comparison, Chandrasekhar found , , , (Chandrasekhar 1969, 110). Darwin was apparently unaware that Liapunov had shown in 1884; see Liapunov (1904, 101) and Liapunov to Poincaré, 12.11.1886 (§ 3-32-3).
— the scale being chosen so that . I enclose a rough drawing
of the section through and , together with your figure — the
ellipsoid being dotted & the pear being in firm line.33
3
The
original drawings have not been located, but were likely those
reproduced in Poincaré’s and
Darwin’s papers (Figs. 1, 2).
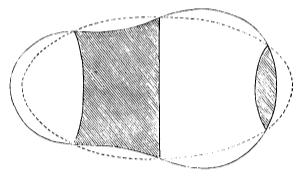 Fig. 1, Poincaré (1885, 347)
Fig. 1, Poincaré (1885, 347)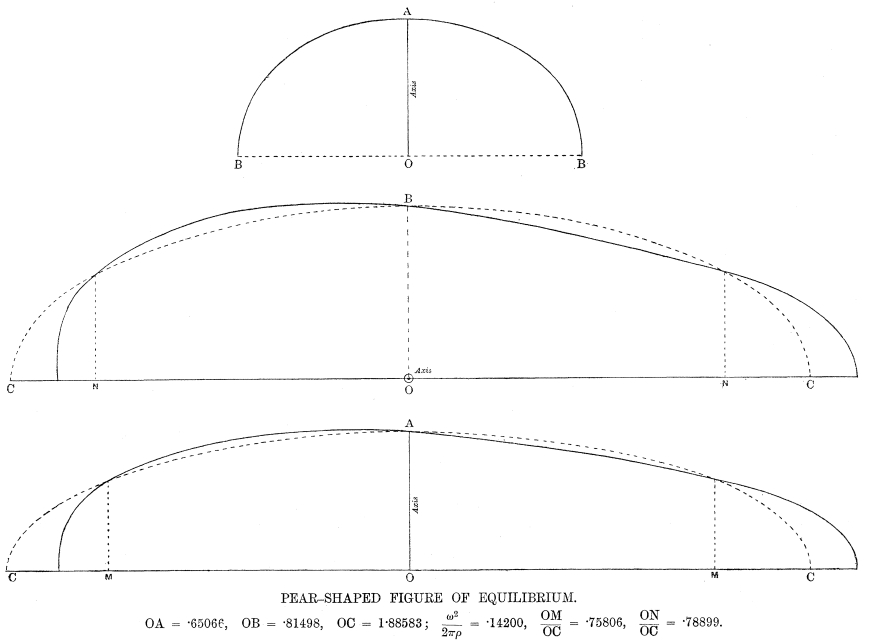 Fig. 2, Darwin (1902b, 329)
Darwin (1902b, 328) stressed that the figure is
considerably longer than Poincaré had supposed. Schwarzschild was
struck by this result, as he wrote to Darwin “Ihr numerisches Resultat
verändert die Anschauung, die man bisher nach Poincaré’s Skizze hatte,
doch sehr wesentlich” (Schwarzschild to Darwin, 22.04.1902,
§ 3-48-6). Schwarzschild
inserted a figure resembling that of Poincaré in his thesis
(Schwarzschild 1896, 46).
Fig. 2, Darwin (1902b, 329)
Darwin (1902b, 328) stressed that the figure is
considerably longer than Poincaré had supposed. Schwarzschild was
struck by this result, as he wrote to Darwin “Ihr numerisches Resultat
verändert die Anschauung, die man bisher nach Poincaré’s Skizze hatte,
doch sehr wesentlich” (Schwarzschild to Darwin, 22.04.1902,
§ 3-48-6). Schwarzschild
inserted a figure resembling that of Poincaré in his thesis
(Schwarzschild 1896, 46).
You probably know that Schwarzschild (Ann. of Munich Ob. vol. III) expressed a doubt as to your conclusion as to the exchange of stabilities in this case.44 4 Poincaré had thought it possible to prove the stability of the pear-shaped figure by an application of the principle of exchange of stabilities (Poincaré 1885, 377–378). Schwarzschild contested Poincaré’s analysis (Schwarzschild 1898, 275), observing that if Poincaré’s figure is rotated 180° about the axis (the axis of rotation in Schwarzschild’s setting; take Poincaré’s original illustration as a section along the -plane), one obtains a figure with the same angular momentum which must be counted as a new figure of equilibrium, since the original figure is not symmetrical with respect to the -plane. The coordinate system rotates with the body, such that a fixed point of the surface of the critical Jacobian is subject to different displacements in the two cases. Consequently, there are two branches of pear-shaped figures starting at the point of bifurcation and extending to the same angular momentum value. Furthermore, one of the two branches of the series of Jacobi ellipsoids extends to the same angular momentum value, such that the angular momentum of the pear-shaped figures determines the stable branch of the Jacobi ellipsoids (i.e, the one with angular momentum lower than that of the critical Jacobian). However, Schwarzschild points out first that the principle of exchange of stabilities applies systematically whenever there are precisely two branches on each side of the point of bifurcation extending to the same angular momentum value (p. 38); and secondly, that the principle applies if and only if a particular coefficient vanishes (p. 40f). The pear-shaped figures belong to the second situation, where the supplementary coefficient is to be studied. Schwarzschild suggested a method involving difficult calculations (p. 45). Poincaré adopted the viewpoint of Schwarzschild (for whom the stability of the pear-shaped figure is a function of angular momentum) in his response to Darwin (§ 3-15-12) and in his article (Poincaré 1902, 333). The reason he assigns (p. 45) is that your figures appear in pairs & that if the figure is turned round it does not reproduce itself. Now it seems to me that he is quite wrong & that it does reproduce itself in the only sense which is material. In my notation (wh[ich] will I think be intelligible to you) the normal displacement which gives the figure is (a zonal surface harmonic of the third order). The investigation of the coefficient of stability shows that it is equally justifiable to take or , and the change of sign of produces the same result as the turning of the figure about the axis of rotation thro’ 180°.55 5 Poincaré (1885) observed that the first point of bifurcation of the Jacobi series occurs when the stability coefficient corresponding to the third zonal harmonic vanishes. Darwin gave the following intuitive explanation of the fact that harmonics of third order are the first harmonics relevant to the problem of the pear-shaped figure: An harmonic of the first order merely denotes a shift of the centre of inertia along one of the three axes; one of the second order denotes a change of ellipticity of the ellipsoid. Since we must keep the centre of inertia at the origin, and since the ellipticity is determined by the consideration that the ellipsoid is a Jacobian, these harmonics need not be considered, and we may begin with those of the third order. (Darwin 1902b, 320) Here the symbol differs from the coefficient of stability encountered in Poincaré (1885). In Darwin’s papers, one finds analogous expressions for the normal displacement (which will also be denoted ) for an arbitrary harmonic (Darwin 1902a, 508; 1902b, 319). In the case of the third zonal harmonic, Darwin evaluates the expression by using formulæ for the evaluation of the functions involved, arriving at an expression involving only the cartesian coordinates , , of the point and the long axis of the critical Jacobian. The role of the quantity (which is designated in the sequel of the correspondence and in Darwin’s paper) is explained by Darwin as follows: The expression has been arranged so that when , , we have . Hence and are the normal displacements at the stalk and blunt end of the pear respectively. (Darwin 1902b, 328)
Thus as I understand it Schwarzschild’s argument breaks down.66 6 A rotation of 180° corresponds to a sign change in the term for the normal displacement, but a fixed point on the surface of the critical Jacobian is subject to different displacements in the two cases, such that the flipped figure is a new figure of equilibrium. I should be very glad if you could let me hear what you think of this. I have several other interesting computations to make & may perhaps come across some other points of interest.
I remain, Yours very sincerely
G. H. Darwin
ALS 2p. Collection particulière, Paris 75017.
Time-stamp: " 7.05.2016 18:29"
References
- Ellipsoidal Figures of Equilibrium. Yale University Press, New Haven. External Links: Link Cited by: footnote 2.
- On Jacobi’s figure of equilibrium for a rotating mass of fluid. Proceedings of the Royal Society of London 41, pp. 319–336. External Links: Link Cited by: footnote 1.
- Ellipsoidal harmonic analysis. Philosophical Transactions of the Royal Society A 197, pp. 461–557. Cited by: footnote 5.
- On the pear-shaped figure of equilibrium of a rotating mass of liquid. Philosophical Transactions of the Royal Society A 198, pp. 301–331. Cited by: footnote 1, footnote 2, footnote 3, footnote 5.
- Sur la stabilité des figures ellipsoïdales d’équilibre d’un liquide animé d’un mouvement de rotation. Annales de la faculté des sciences de Toulouse 6 (1), pp. 5–116. External Links: Link Cited by: footnote 2.
- Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Acta mathematica 7 (1), pp. 259–380. External Links: Link Cited by: footnote 1, footnote 3, footnote 4, footnote 5.
- Sur la stabilité de l’équilibre des figures piriformes affectées par une masse fluide en rotation. Philosophical Transactions of the Royal Society A 198, pp. 333–373. External Links: Link Cited by: footnote 4.
- Die Poincarésche Theorie des Gleichgewichts einer homogenen rotierenden Flüssigkeitsmasse. Ph.D. Thesis, Ludwig-Maximilians-Universität zu München, Munich. Cited by: footnote 3.
- Die Poincaré’sche Theorie des Gleichgewichts einer homogenen rotierenden Flüssigkeitsmasse. Neue Annalen der königlichen Sternwarte in Bogenhausen bei München 3, pp. 231–299. External Links: Link Cited by: footnote 4.
- Treatise on Natural Philosophy. Cambridge University Press, Cambridge. External Links: Link Cited by: footnote 1.