2-17-3. H. Poincaré to Victor Crémieu

[Ca. 08–09.1901]

Question de secteur chargé tournant en face d’une nappe fixe dont les 2 extrémités sont reliés à un galvanomètre.¹¹ 1 L’absence de forme d’adresse, et les ratures du manuscrit témoignent d’une certaine rapidité de rédaction.

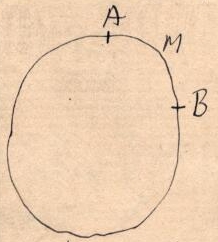
	$\ell$ , longueur totale du circuit
	$x$ , longueur $A M B$ .
	$i=\varphi(x,t)$ , intensité au point $B$ .
	$i_{0}=\varphi(0,t)$ , intensité au point $A$ .
	$Q$ , charge de la section $A M B$ .
	$\varrho dx$ , résistance du segment $d x$ .
	$V$ , potentiel; $R$ résistance totale du circuit.

On a :

i\varrho dx=dV\text{ (loi de Ohm)}

ou en étendant l’intégrale au circuit tout entier

	$\displaystyle\int i\varrho dx$	$\displaystyle=0.$	(1)
On a
	$\displaystyle i-i_{0}$	$\displaystyle=\frac{dQ}{dt},$	(2)
d’où
	$\displaystyle 0=\int i\rho dx$	$\displaystyle=\int\frac{dQ}{dt}\varrho dx+i_{0}\int\rho dx$	(3)
d’où :
	$\displaystyle i_{0}$	$\displaystyle=-\frac{1}{R}\int\frac{dQ}{dt}\rho dx.$

Or $Q$ est une fonc. périodq. du temps. Donc la valeur moyenne de $dQ/dt$ est nulle. Donc il en est de même de celle de $\int{\frac{dQ}{dt}\varrho dx}$ donc de celle de $i_{0}$ , donc de celle de $i$ C.Q.F.D.

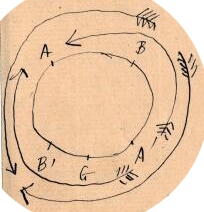
J’arrive au cas symétrique que vous supposiez la dernière fois. Le galvanomètre est en $G$ , la nappe en $A B$ .

$A^{\prime}$ et $B^{\prime}$ sont diamétralement opposés à $A$ et à $B$ .

Au moment où le secteur fixe vient en $A$ nous avons charge, au moment où il vient en $B$ nous avons décharge. Les courants de charge compensent-ils ceux de décharge.

Le sens des courants de charge est indiqué par les flèches intérieures, le sens des courants de décharge par les flèches extérieures. Vous voyez qu’en $G$ les deux courants sont de même sens.

Ces deux courants sont bien égaux mais pas de sens contraire.

Coëff. d’induc.

Je crois que pour le calcul de $M$ , vous pouvez vous contenter des formules approchées suivantes :

Je représente ici en $A$ et en $B$ la section de l’un des circuits par le plan de symétrie en $C$ et en $D$ celle de l’autre circuit. J’appelle $\varrho$ la distance $C A$ . Le coëff. $M$ sera :

K\log\varrho+C=M

$C$ et $K$ étant des constantes qui dépendent des arcs des deux cercles $A B$ et $C D$ qui entrent en jeu et des rayons du cercle $A B$ .

1°Si les deux cercles sont complets, on a : pour le coëff. d’induction de deux cercles très rapprochés, rayon des deux cercles $a$ , distance des deux circuits $=\varrho$ ; on a dis-je :

M=4ra\log\frac{8a}{\rho}-8ra.

2°Si l’un des cercles est complet et l’autre a un angle $\varphi$ , on a :

M=2\varphi a\log\frac{8a}{\rho}-4\varphi a.

3°Pour deux cercles incomplets, les formules deviennent assez compliquées et je crois que vous pouvez vous contenter de la précédente. La différence ne serait pas grande. Si nous supposons alors une nappe ; et que nous nous contentions de cette expression simplifiée nous trouvons encore quelque chose d’assez compliqué. Soit $x_{0}$ le rayon extérieur de la nappe, $y$ celui de la spire induite, $x_{1}$ le rayon intérieur :

x_{0}>y>x_{1}.

On trouve : non, je ne transcris pas cette formule qui est trop compliquée;²² 2 Variante : “On trouve : $\frac{M}{3}(x_{0}^{3}-x_{1}^{3})=$ ; non, je ne transcris pas cette formule qui est trop compliquée ; il suffira de se rappeler que la seule fraction. il m’en vient … ”. La formule est barrée. il m’en vient une autre à l’esprit qui est plus simple, et dont je vous parlerai longuement une autre fois après y avoir un peu réfléchi. Mais elle me fait voir facilement une limite supérieure de $M$ et je suis frappé de voir combien cette limite est petite; elle est de l’ordre de $10^{-8}$ Henry multiplié par le nombre des spires.

N’y aurait-il pas lieu de demander quelques détails à Pender ?³³ 3 Poincaré écrira lui-même à Pender en 1902 (§ 2-45-1).

Tout à vous,

Poincaré

ALS 4p. Archives de l’Académie des sciences de Paris.

Time-stamp: "19.03.2015 01:57"