3-15-3. George Howard Darwin to H. Poincaré

20.3.99

Newnham Grange–Cambridge

Dear Monsieur Poincaré,

I think you will be interested to learn that I have at last discovered (as I believe with confidence) the natural history, so to speak, of the $A$ orbits & the figure-of-8 which I will call $A^{\prime }$. Somewhere between $C=40$ & $39.6$ an orbit of ejection which is periodic arises of this form:

As $C$ falls in value the loop diminishes becomes a cusp & then becomes rounded & coalesces with $A$ when both vanish.

For a very slightly smaller value of $C$ another orbit of ejection arises of this form:

In this case also the loop diminishes, becomes a cusp, then rounded & we pass on to the figures-of-8 $A^{\prime }$ which I have traced.

I missed these families because they have so transitory an existence. I have my idea of how they will behave as to stability.

Now pass to the side of $J$ remote from $S$ & it is obvious that the $C$ orbit ends in an orbit of ejection thus:

For a very slightly smaller value of $C$ a new orbit of ejection arises thus:

(I should have drawn the other half of these.)

This orbit is obviously the parent of a new series of figures-of-8 thus

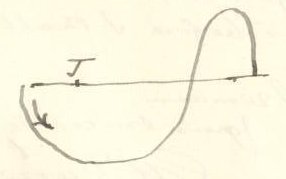
The quasi-coalescence & disappearance of the figure-of-eight $A$ (or say $A^{\prime }$) with $B$ may take place through the figure-of-8 terminating in an orbit of ejection, & $B$ with another. But I have not yet the materials for deciding this point. These ideas throw a flood of light on the march of the orbits, but I will not trouble you with more.

I think I shall ask Mittag Leffler to let me have another paper in the Acta but I fear it will be some months before I shall be ready.

I remain, Yours sincerely

G. H. Darwin

ALS 4p. Collection particulière, Paris 75017.

Time-stamp: "14.01.2016 03:44"