Introduction: La Correspondance d’Henri Poincaré, Vol. 2

Le rôle de la physique mathématique est de bien poser les questions,

ce n’est que l’expérience qui peut les résoudre.

Poincaré à Pierre Weiss, ca. novembre 1911

L’intérêt que portait Henri Poincaré (1854–1912) à des questions d’ordre physique a été durable et profond; elle couvre presque toute sa carrière, et marque l’histoire de la physique tout au long du 20^e siècle. Cet intérêt pose un défi à la compréhension, d’une part, parce que la carrière de Poincaré ne ressemble à celle d’aucun de ses contemporains, rendant caduque l’approche comparatiste. D’autre part, Poincaré ne travaille pas exclusivement sur des problèmes de physique, mais se penche en même temps sur d’autres questions sans rapport apparent: des questions d’analyse, de topologie, de géométrie, de mécanique céleste, d’électrotechnique, et de philosophie des sciences. Qu’il existe des fils communs entre ces disciplines disparates, Poincaré nous l’affirme, et il en identifie certains lui-même dans son “analyse des travaux” (Poincaré 1921). L’identification et la localisation de ces fils préparent la détermination de leur fonction dans la pratique scientifique de Poincaré. Dans cette optique, l’étude des cahiers de recherche et de la correspondance scientifique offre un éclairage certain.

On peut s’interroger également sur la nature des liens que Poincaré forme avec ses collègues physiciens, ainsi que sur son appartenance à la communauté de physiciens. Encore une fois, sa correspondance représente une source essentielle pour l’étude de ces questions. Les lettres que nous publions dans ce volume n’étaient pas, pour la plupart, destinées à la publication. Elles nous font entrer dans le cercle des connaissances de Poincaré, avec des amis de longue date, tels Henri Becquerel et René Blondlot. En dehors de ce cercle, Poincaré se fait connaître en tant que physicien surtout à travers ses cours et publications, et ses activités académiques et professionnelles. Afin de faciliter la comparaison des faces publique et privée de Poincaré, nous rappellerons les grandes lignes de la carrière de Poincaré en physique, ses lieux de publication, avant d’analyser la place de ses échanges avec des physiciens, chimistes et ingénieurs par rapport à l’ensemble de sa correspondance.

La carrière de Poincaré en physique

La réputation scientifique de Poincaré se construit d’abord en mathématiques pures, à travers sa découverte des fonctions fuchsiennes, ses travaux sur les séries divergentes et le problème restreint des trois corps, et ses contributions en topologie algébrique, qui font de lui le premier mathématicien de son temps, reconnu comme tel par ses pairs. En même temps, au tournant du vingtième siècle, Poincaré figure parmi les meilleurs physiciens théoriciens. Il est d’ailleurs le seul Français, avec Joseph Boussinesq, à atteindre ce niveau, alors qu’en physique expérimentale font autorité les travaux d’Henri Becquerel, Alfred Cornu, Pierre et Marie Curie, Georges Gouy, Jean Perrin, et Pierre Weiss. La réputation de physicien se construit chez Poincaré d’abord à partir de ses cours d’optique mathématique (1887–1888), et sur une lecture pénétrante de la théorie électromagnétique de Maxwell, transmise dans les cours professés en 1888 et 1890, l’année intercalaire étant celle d’un cours sur le problème des trois corps. Son volume sur la théorie de Maxwell fait date, étant le premier à paraître en Allemagne, et le deuxième en France, après les traductions de Maxwell.

Poincaré souligne la puissance de l’approche lagrangienne de Maxwell; il démontre en passant (Poincaré 1890, xiv) une remarque de ce dernier selon laquelle, si un phénomène admet une explication mécanique complète, il admet une infinité d’autres, toutes aussi compatibles avec l’expérience. En même temps, il transforme la théorie du fluide unique de Maxwell en théorie de deux fluides, et il déforme ses notions de charge et de courant électrique. Au pays de Helmholtz et de Hertz, où la nouvelle sous-discipline de physique théorique devient autonome, les cours de Poincaré, avec leur démarche inductive et leur exposition mathématique élégante, servent de modèle pédagogique, comme l’observe O. Darrigol (1993). Au pays de Maxwell, G.F. FitzGerald déplore une présentation trop mathématique des questions physiques (Nature, 1892, 45), mais l’approche de Poincaré séduit d’autres britanniques (dont A. Gray et J. Jeans), et l’aisance de son exposition mathématique suscite l’admiration générale. Pourtant, aucun traité de physique de Poincaré n’est traduit en anglais, alors que trois volumes sont traduits en allemand. En général, l’approche inductive et lisse de Poincaré séduit aussi bien des physiciens britanniques que continentaux, et promeut la théorie de Maxwell et la mécanique lagrangienne.

En électrodynamique maxwellienne Poincaré (1891) est parmi les premiers à appliquer des potentiels retardés, et les ingénieurs lui doivent une méthode d’intégration de l’équation des télégraphistes (1893). Dans une contribution fondamentale, Poincaré (1900) montre la contradiction entre la mécanique newtonienne et la théorie des électrons de H.A. Lorentz, une théorie qu’il rend plus plausible en trouvant une interprétation physique d’un artifice mathématique, le temps local. Cinq ans plus tard, il intervient de nouveau, afin de rendre compatible la théorie de Lorentz avec le principe de relativité. Mais à la différence d’Einstein, il retient la notion d’un éther luminifère, ce qui lui permet de se passer du postulat d’isotropie de la lumière. Il caractérise, en même temps, l’algèbre de Lie du groupe de Lorentz, et il dérive les deux premières lois de la gravitation covariantes par rapport aux transformations de Lorentz. Ce faisant, il trouve les quadrivecteurs qui serviront à la théorie de l’espace-temps de Minkowski (1908), dont il déplorera l’interprétation einsteinienne des coordonnées spatio-temporelles, leur préférant une convention interprétative équivalente à la postulation de l’espace-temps de Galilée (S. Walter 2009).

Alors que ces contributions sont reconnues du vivant de Poincaré, son intégration à la communauté des physiciens ne va pas de soi. D’un point de vue institutionnel, Poincaré apparaît bien comme l’un des maîtres de la physique mathématique française, en tant que professeur de physique mathématique à la faculté des sciences de Paris, une chaire qu’il occupe entre 1886 et 1896. Il l’abandonne à la mort de l’astronome Félix hreftisserand.htmlTisserand, pour celle d’astronomie mathématique et de mécanique céleste, sans délaisser l’enseignement de sujets physiques. Il garde son intérêt pour la recherche en physique, surtout en ce qui concerne l’électrodynamique. En 1898, il est admis à la Société française de physique, avant d’être élu à la présidence de cette société en 1902.

Les titres de Poincaré en mathématiques, physique théorique, mécanique céleste, et philosophie des sciences sont reconnus par presque toutes les académies scientifiques en Europe et aux États-Unis au début du vingtième siècle. La communauté mathématique est unanime dans sa reconnaissance de ses contributions, l’étendue et la profondeur desquelles personne ne peut espérer à imiter. Cette domination intellectuelle n’a pas de pendant à l’Académie des sciences, où Poincaré se montre moins habile que d’autres dans la réalisation de ses projets. Élu président de l’Académie des sciences en 1906, l’année suivante Poincaré présente sa candidature au poste de secrétaire perpétuel pour les sciences physiques, en remplacement de Marcelin Berthelot. Alors qu’il devait remporter le scrutin par une faible majorité des voix, Poincaré préfère retirer sa candidature, au profit de celle du minéralogiste Albert de Lapparent.

Poincaré essuie un deuxième échec en 1910, lorsqu’il mène campagne pour le prix Nobel de physique, avec l’assistance énergique du mathématicien suédois G. Mittag-Leffler. Sa candidature bénéficie d’un nombre record de lettres de soutien, mais elle rencontre l’opposition de deux physiciens de Cambridge, J.J. Thomson et E. Rutherford (Crawford 1984). Plus surprenant est l’appui très faible de la part des néerlandais H.A. Lorentz et P. Zeeman (§ 62.28), bénéficiaires tous les deux du soutien très fort de Poincaré lors de la campagne de 1902 (§ 62.8).

D’où vient cette hésitation à admettre Poincaré dans le cercle des physiciens ? Sa formation initiale n’est pas en cause : en tant qu’ancien élève de l’École polytechnique (promotion de 1873), et de l’École des mines, Poincaré a suivi une voie tracée par deux membres de la section de physique générale de l’Académie des sciences: son ancien professeur de physique Alfred Cornu (promotion de 1867), et Henri Becquerel (promotion de 1872), lauréat du prix Nobel (1903). Comme l’observe P. Galison (2003), Poincaré porte la “marque de fabrique” de sa formation polytechnicienne, un pragmatisme d’ingénieur d’état, qui sait analyser un problème dans toutes ses facettes, rassembler toutes les ressources à sa disposition, et en fonction de ces éléments, choisir la solution optimale. À la différence de Cornu et Becquerel, Poincaré soutient une thèse en mathématiques (sur la théorie géométrique des équations différentielles), et ses premières publications le marquent aux yeux des savants comme un mathématicien de premier ordre, comme l’observe C. Gilain (1977). En 1885, lorsque Poincaré est nommé chargé du cours de mécanique physique et expérimentale à la Sorbonne, il n’a rien publié dans ces domaines, ce que M. Atten (1988) explique par la mainmise institutionnelle des mathématiciens sur les postes de physique. L’année suivante, Poincaré est élu président de la Société mathématique de France, et il devient professeur de physique mathématique et calcul des probabilités à la Sorbonne. Quelques mois après sa nomination, il est présenté en première ligne par la section de géométrie à l’Académie des sciences. A l’âge de 32 ans, quatre semaines avant son élection, il publie sa première note de physique mathématique, sur la distribution de l’électricité (Poincaré 1887).

Poincaré garde la chaire de physique pendant dix ans avant de faire un échange, à la demande du doyen Darboux, pour celle d’astronomie mathématique et mécanique céleste. Entre 1886 et 1901 il publie dix-sept volumes et 80 articles de physique mathématique, mais pour ses collègues physiciens, ces contributions ne font pas de lui un simple physicien. Au mieux, comme le veut le professeur de physique générale et mathématique au Collège de France Marcel Brillouin (1901, 127), Poincaré devient un “physicien-géomètre”. Ayant quitté la chaire de physique, Poincaré essaie de s’intégrer davantage dans la communauté des physiciens. Il devient membre de la Société française de physique, entre au conseil de l’Éclairage électrique, prend en charge le cours d’électricité théorique à l’École supérieure des postes et télégraphes, et en 1902, il préside la Société française de physique. Néanmoins, il n’arrive pas à se défaire de l’étiquette collée par Brillouin. Au centenaire de la naissance de Poincaré, par exemple, Louis de Broglie (1954, X) le décrit comme “plus analyste que physicien.”

La remarque de de Broglie vise le style de Poincaré en physique théorique, et souligne une différence par rapport à la pratique de ses contemporains. Si on considère la physique comme elle se fait en France au début du 20^e siècle, Poincaré se situe à l’un des deux extrêmes d’une droite qui va de la physique mathématique à la physique expérimentale, à une époque où la physique française se veut surtout expérimentale. La revue de physique dominante, le Journal de physique théorique et appliquée ne publie que de rares études théoriques au début du 20^e siècle (en dépit de son titre), et néglige la recension d’articles théoriques parus à l’étranger. Il faudra attendre jusqu’à la fin des années 1920 pour voir l’émergence modeste de la physique théorique à Paris, comme le montre D. Pestre (1992, 119).

Figure singulière par sa réussite en mathématiques et en physique, Poincaré le paraîtrait davantage sans doute si on prenait en compte ses contributions en philosophie des sciences et en mécanique céleste. Dans la section suivante, nous essayons de cerner d’une manière quantitative l’activité en physique de Poincaré par rapport aux autres disciplines.

Les lieux de publication

En face d’une œuvre dense, variée et importante (dix tomes d’articles de recherche, cinq volumes philosophiques, vingt-quatre volumes de cours), les commentateurs de Poincaré ont fait le choix de découper leur sujet selon des lignes disciplinaires. Dès la mort du savant en 1912, ses collègues ont publié des comptes-rendus intitulés “Poincaré mathématicien,” “Poincaré astronome”, “Poincaré physicien”, et “l’œuvre philosophique”. Ces découpages vont à l’encontre de la philosophie de Poincaré, qui cherche à rapprocher les sciences exactes. Selon lui (Poincaré 1897) la physique mathématique et l’analyse pure “se pénètrent mutuellement, et leur esprit est le même.” Malgré cette interpénétration, les revues de recherche se distinguent souvent par la nature des articles qu’elles accueillent. A partir de ce fait, une première carte disciplinaire de l’activité scientifique de Poincaré se dessine à travers un classement disciplinaire des revues dans lesquelles il publie ses écrits.

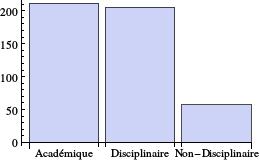
Notre analyse se base sur la bibliographie de Poincaré. Pour les besoins de l’analyse, nous prenons trois catégories distinctes de revues : académique (par exemple, les Comptes rendus hebdomadaires de l’Académie des sciences), disciplinaire (par exemple, le Journal de physique théorique et appliquée), et généraliste (comme la Revue générale des sciences pures et appliquées). Nous négligeons les livres de Poincaré, ainsi que les articles parus en tant que chapitres de livres.

La figure (1) montre que Poincaré publie à peu près aussi fréquemment dans les organes de publication académiques que dans les revues disciplinaires. Très souvent, en fait, les articles académiques fournissent le résumé d’un mémoire publié dans une revue disciplinaire. Le nombre de publications non-disciplinaires est relativement faible (10%), mais les titres qui y figurent sont publiés une seule fois dans une revue, alors que les titres disciplinaires sont réédités parfois : une fois dans une revue disciplinaire, et une ou plusieurs fois dans des revues généralistes. Par exemple, Poincaré publie l’article “L’invention mathématique” une fois dans une revue disciplinaire (l’Enseignement mathématique), une fois dans une revue généraliste (la Revue générale des sciences pures et appliquées), et après quelques retouches, dans son livre Science et méthode (Poincaré 1908).

Figure 1. Articles de Poincaré (N = 472).

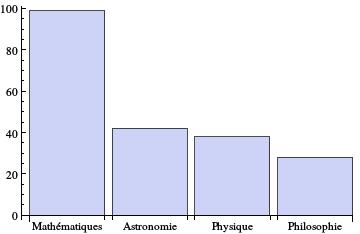
Pour obtenir une idée de la distribution disciplinaire des publications de Poincaré, divisons la catégorie disciplinaire de la figure (1) en quatre sous-catégories : les mathématiques, l’astronomie, la philosophie, et la physique pure et appliquée. Nous obtenons ainsi la figure (2). L’établissement des trois premières catégories va de soi, alors que la quatrième, la physique pure et appliquée, nécessite des précisions. Pendant toute sa carrière, Poincaré ne publie que quatre articles dans des revues de recherche en physique. D’où viennent donc les 37 autres articles de la catégorie “physique” ? Vingt-neuf d’entre eux paraissent dans un journal destiné aux ingénieurs électriciens, l’Éclairage électrique, ou son successeur, la Lumière électrique. Poincaré appartient au comité de rédaction de ces revues, et par ses contributions il participe à la formation des ingénieurs électriciens.

La figure (2) montre que Poincaré publie deux fois plus fréquemment dans des revues de mathématiques que dans des revues de physique ou d’astronomie, et presque quatre fois plus fréquemment que dans des revues philosophiques. A partir du fait que Poincaré publie de nombreux articles dans une revue généraliste comme la Revue générale de sciences pures et appliquées (64 titres), on pourrait être tenté de conclure qu’il cherchait à brouiller les pistes disciplinaires. Pourtant, seulement trois articles disciplinaires sont publiés dans deux revues de discipline hétérogène, par exemple, de physique et de philosophie.

Figure 2. Articles de Poincaré publiés dans une revue disciplinaire (N = 205).

Classe	Tome	Classe	Tome
Analyse	I, II, III	Topologie	VI
Géométrie	IV	Mécanique céleste et astronomie	VII, VIII
Algèbre	V	Physique mathématique	IX, X

Table 1. La tomaison des Œuvres de Poincaré (Darboux et al., dirs., 1916).

La biographie de Poincaré éclaire également les détails de la distribution de ses publications mathématiques dans la catégorie des revues de mathématiques. L’amitié entre Poincaré et le rédacteur en chef des Acta mathematica, Gösta Mittag-Leffler, a sans doute motivé Poincaré à publier plus d’articles fondamentaux dans cette revue qu’ailleurs (c’est-à-dire, 30% de ses publications mathématiques). La même remarque pourrait se faire à propos des Rendiconti di Palermo de G.B. Guccia, où Poincaré publie 15% de ses articles mathématiques. En plus des revues précitées, Poincaré est membre des comités de rédaction du Journal de physique, du Bulletin de la Société mathématique de France, et du Journal de mathématiques pures et appliquées.

On peut comparer les données disciplinaires de la figure (2) avec la classification effectuée par les éditeurs des dix premiers tomes des Œuvres de Poincaré, parus entre 1916 et 1954. Ces éditeurs ont réédité et associé des sélections d’articles indépendamment de leur provenance. Comme on voit dans la table (1), en reprenant la distribution des articles dans les Œuvres, la physique mathématique représente 20% de l’ensemble, qui correspond bien à la proportion d’articles disciplinaires parus dans des revues de physique (19%, ou 38 sur 205), qu’on voit représentés dans figure (2).

La correspondance

La correspondance de Poincaré offre une image détaillée de son activité scientifique, aussi bien par les renseignements bruts qu’elle nous fournit sur le nombre, la qualité et la distribution spatio-temporelle de ses correspondants, qu’à travers les discussions vivantes dont les lettres sont une trace, et souvent la seule qui nous reste.

L’inventaire de sa correspondance fait état de 372 correspondants pour 1890 lettres, plus une vingtaine de lettres dont le correspondant est inconnu. L’ensemble de correspondants scientifiques le plus important est celui des mathématiciens, avec 99 individus. (Pour les besoins de l’analyse, un mathématicien est quelqu’un qui enseigne les mathématiques au lycée ou à l’université.)

Après les mathématiciens viennent les physiciens. Qui sont-ils, et pourquoi les avoir mis ensemble dans ce volume, à l’exclusion d’autres correspondants? Parmi une soixantaine de correspondants figurant dans ce volume, on trouve cinq chimistes, cinq ingénieurs, et cinquante-et-un physiciens, si on admet une définition suffisamment large de ce dernier métier. Nous admettons en tant que physicien tout professeur de physique générale, électricité, physique mathématique, ou mécanique rationnelle. Cette définition comprend 45 des 51 correspondants physiciens; les six autres ont tous publié sur des questions de physique. Certains correspondants physiciens font de la chimie et de la physique, comme Svante Arrhenius, et le couple Curie, si bien qu’une distinction entre les deux disciplines a peu de sens. Il en va de même pour des correspondants comme André Blondel, ingénieur au service des phares, avant d’être professeur d’électricité au conservatoire national des arts et métiers. Poincaré, lui aussi, commence sa vie professionnelle comme ingénieur (des mines), avant d’intégrer la faculté des sciences de Caen en tant que chargé de cours d’analyse (1880); il enseignera par la suite à la Sorbonne l’analyse (1881), la mécanique physique et expérimentale (1885), avant d’être nommé à la chaire de physique mathématique et calcul des probabilités (1886), comme nous l’avons déjà mentionné.

Une troisième catégorie disciplinaire concerne les astronomes et géodésiens, comprenant tous ceux qui enseignent l’astronomie ou sont affiliés à un observatoire ou un service des cartes (comme le bureau de longitudes à Paris). Tous les autres correspondants de Poincaré, y compris les philosophes, les membres de sa famille, les agents administratifs, les homme politiques, figurent dans une catégorie à part (“Autre”).

	Mathématiques	Phys./Chim./Ing.	Astronomie	Autre	Total
Individus	99	61	44	171	375
% du total	26	16	12	46	100

Table 2. La distribution disciplinaire des correspondants de Poincaré.

Poincaré compte presqu’autant de correspondants mathématiciens (99) que de correspondants physiciens, chimistes, ingénieurs et astronomes ensemble (105). Néanmoins, un correspondant sur quatre est mathématicien, ce qui est une mesure de l’implication de Poincaré dans des activités autre que celles liées aux mathématiques.

Prenons ensuite l’ensemble de la correspondance passive avec des physiciens, chimistes, et ingénieurs. Alors qu’un correspondant sur trois dans cet ensemble est théoricien, les trois échanges les plus suivis concernent les expérimentateurs : l’universitaire nancéien René Blondlot (29 lettres passives), un écrivain touche-à-tout, Gustave Le Bon (21 actives, 3 passives), et le jeune Victor Crémieu (18 lettres actives, 3 lettres passives). Les échanges avec des théoriciens ne sont pas négligés par Poincaré, mais ils ne sont pas aussi riches. Les trois échanges les plus importants avec des théoriciens sont ceux avec Alfred Potier (3 actives, 17 passives), William Thomson (6 actives, 11 passives), et Heinrich Hertz (6 actives, 9 passives).

La correspondance avec Hertz est remarquable à plus d’un titre, mais il y a un détail en particulier qui la distingue des autres: Poincaré prend soin d’écrire la date de sa lettre, alors qu’il la néglige systématiquement ailleurs. Croyait-il que sa correspondance avec Hertz devait être éditée un jour? Qu’en est-il alors des autres? Quoi qu’il en soit, l’inventaire de la correspondance de Poincaré montre qu’il entretenait pendant presque toute sa carrière scientifique un réseau de physiciens français et étrangers, dont l’existence confère un sens à la sélection de correspondants physiciens, chimistes et ingénieurs contenue dans ce volume.

Scott A. Walter

Nancy

Décembre 2006

Time-stamp: "30.12.2016 00:49"