H. Poincaré: Über die Reduktion der Abelschen Integrale und die Theorie der Fuchsschen Funktionen

Meine Herren! Ich habe die Absicht, Ihnen heute über die Reduktion der Abelschen Integrale im Zusammenhang mit der Theorie der automorphen und insbesondere der Fuchsschen Funktionen vorzutragen.

Ein System von Abelschen Funktionen von $p$ Variabeln und $2p$ Perioden heißt reduzibel, wenn es sich auf ein System von $q$ Variabeln und $2q$ Perioden zurückführen läßt. Hierbei ist es von vornherein von Wichtigkeit, zwei Fälle zu unterscheiden:

Im ersten Falle soll es möglich sein, das System $S$ Abelscher Funktionen von $p$ Variabeln durch eine algebraische Kurve $C$ vom Geschlechte $p$ zu erzeugen. Ebenso soll das System $S^{\prime }$ von $q$ Variabeln aus der Theorie eines algebraischen Gebildes vom Geschlechte $q$ entspringen.

Dieser unser erste Fall ist aber bekanntlich nicht der allgemeine; denn die Kurve $C$ hängt nur von $3p-3$ Konstanten ab, während die allgemeinen Abelschen Funktionen von $p$ Variabeln $\frac{p\left(p+1\right)}{2}$ Parameter enthalten. Dadurch ist der zweite der beiden Fälle gegeben, die wir unterscheiden. In diesem Falle nämlich soll mindestens eines der beiden Systeme $S$, $S^{\prime }$ nicht aus der Theorie der algebraischen Gebilde entspringen.

In meinem heutigen Vortrag will ich mich durchaus auf den erstgenannten Fall beschränken. Aber auch dann muß ich noch zwei Fälle unterscheiden. Wir knüpfen nämlich unsere Betrachtungen an die beiden algebraischen Kurven $C$ und $C^{\prime }$ an. Im Falle der Reduzibilität besteht zwischen beiden eine algebraische Korrespondenz. Die Beschaffenheit derselben liegt der in Aussicht gestellten Fallunterscheidung zugrunde.

Der erste Fall ist der folgende. Vermöge der Korrespondenz ist jedem Punkte $M$ von $C$ ein und nur ein Punkt $M^{\prime }$ von $C^{\prime }$ zugeordnet, während umgekehrt jedem Punkte von $C^{\prime }$ $n$ Punkte von $C$ entsprechen. Ich nenne dann $n$ die charakteristische Zahl der Korrespondenz und sage, $C$ ist eine vielfache Kurve von $C^{\prime }$.

Der eben genannte erste Fall ist aber nicht der allgemeine. Das ist vielmehr der nun folgende zweite. Hier nämlich besteht die Korrespondenz nicht zwischen einzelnen Punkten $M$ und $M^{\prime }$, sondern zwischen Systemen von Punkten $M_1,\mathrm{\dots },M_{\nu }$ von $C$ mit den Koordinaten $x_1,y_1;\mathrm{\dots };x_{\nu },y_{\nu }$ und $M_1{}^{\prime },\mathrm{\dots },M_{\nu }{}^{\prime }$ von $C^{\prime }$ mit den Koordinaten $x_1{}^{\prime },y_1{}^{\prime };\mathrm{\dots };x_{\nu }{}^{\prime }y_{\nu }{}^{\prime }$. Jedem System auf $C$ soll dabei ein und nur ein System auf $C^{\prime }$ entsprechen, während umgekehrt einem System auf $C^{\prime }$ im allgemeinen mehrere Systeme auf $C$ zugeordnet sind. Ich sage dann, $C$ ist eine pseudovielfache Kurve von $C^{\prime }$.

Im erstgenannten Falle sind $x^{\prime }$ und $y^{\prime }$ rationale Funktionen von $x$ und $y$, während im zweiten nur geschlossen werden kann, daß jede rationale und symmetrische Funktion der $(x_1{}^{\prime }y_1{}^{\prime },\mathrm{\dots },x_{\nu }{}^{\prime }y_{\nu }{}^{\prime })$ eine rationale Funktion der $(x_1{y}_1,\mathrm{\dots },x_{\nu }{y}_{\nu })$ ist. Es ist leicht zu sehen, daß jede Kurve $C$, die eine vielfache von $C^{\prime }$ ist, auch eine pseudovielfache der Kurve $C^{\prime }$ ist. Umgekehrt aber habe ich mehrere Beispiele bilden können dafür, daß nicht jede pseudovielfache Kurve von $C^{\prime }$ auch eine vielfache von $C^{\prime }$ ist. Ich will jedoch hier nicht näher darauf eingehen, zumal da sich meine folgenden Darlegungen durchaus an den ersten Fall anschließen werden.

Im Falle der Reduzibilität unserer Integrale ist es möglich, ihre Periodentabelle auf eine besondere Normalform zu bringen. Die folgenden beiden Beispiele mögen eine Anschauung von der Beschaffenheit derselben geben.

1) $q=1$; $p=3$. Die Periodentabelle kann auf die folgende Form gebracht werden:

2) $q=2$; $p=4$. Die normierten Perioden sind hier:

Die Zahlen $\alpha$, $\beta$ bedeuten in beiden Tabellen ganze rationale Zahlen.

Ich definiere nun noch eine zweite charakteristische Zahl $\kappa$. Sie gibt die Ordnung der Thetafunktion von $q$ Variabeln an, in die eine Thetafunktion erster Ordnung von $p$ Variabeln im Falle der Reduzibilität transformiert werden kann. Im ersten Beispiel ist $\kappa =\alpha$, im zweiten $\kappa =\alpha \beta$. Die beiden charakteristischen Zahlen $n$ und $\kappa$ sind nun immer einander gleich. Ich habe zwei Beweise für diesen Satz gefunden, die ich jetzt in ihren Grundzügen auseinandersetzen will.

Erster Beweis. Seien $M$ und $M^{\prime }$ zwei Abelsche Integrale erster, zweiter oder dritter Gattung der Kurve $C$. Ich denke mir die zugehörige Riemannsche Fläche irgendwie längs $2p$ von einem Punkte ausgehenden nichtzerstückenden Rückkehrschnitten kanonisch aufgeschnitten. Dann mögen $M$ und $M^{\prime }$ die folgenden Perioden besitzen:

$M$ $:x_1,x_2,\mathrm{\dots },x_{2p},$

$M^{\prime }$ $:y_1,y_2,\mathrm{\dots },y_{2p}.$

Ich muß nun eine charakteristische fundamentale Bilinearform definieren. Ich setze nämlich:

$$F(x,y)=\int M𝑑M^{\prime }$$

wo das Integral längs der ganzen Kontur der Zerschneidung erstreckt werden soll. Wenn $x$, $y$ Normalperioden sind, so nimmt $F(x,y)$ die folgende Form an:

$$F(x,y)=\sum _{\kappa =1}^p\left(x_{2\kappa -1}{y}_{2\kappa }-x_{2\kappa }{y}_{2\kappa -1}\right).$$

Nehme ich an, es sei $M$ eines der reduziblen Integrale, dann drücken sich seine $2p$ Perioden ganzzahlig und linear durch nur $2q$ Perioden ${\omega }_1,\mathrm{\dots },{\omega }_{2q}$ aus. Ich habe also dann:

$x_{\kappa }={\displaystyle \sum _{j=1}^{2q}}{m}_{\kappa j}{\omega }_j$ $(\kappa =1,2,\mathrm{\dots },2p),$

wo die $m_{\kappa }$ ganze rationale Zahlen bedeuten. Wenn nun $M$ und $M^{\prime }$ Integrale erster Gattung sind, dann ist bekanntlich

$$F(x,y)=0$$

Wenn man in diese Gleichung die Ausdrücke der $x$ durch die $\omega$ einsetzt, so bekommt man eine bilineare Gleichung zwischen den $y$ und $\omega$, die in der folgenden Form geschrieben werden kann:

$$\sum _{j=1}^{2q}{H}_j{\omega }_j=0$$

Seien nun $u_1,\mathrm{\dots },u_p$ $p$ linear unabhängige Integrale erster Gattung von $C$. Dann können wir setzen:

Die vorläufig noch unbestimmten Koeffizienten ${\mu }^{\prime }$ sollen nun so bestimmt werden, daß sie den $2q$ linearen Gleichungen:

$H_j=0$ $(j=1,2,\mathrm{\dots },2q)$

genügen. Wenn man dann noch beachtet, daß diese $2q$ Gleichungen nicht linear unabhängig sind, sondern daß zwischen ihnen $q$ Relationen

$$\sum H_j{\omega }_j=0$$

bestehen, so ist leicht zu erkennen, daß auch $M_1$ reduzierbar ist, und daß, so wie $M$ einer Schar von $q$ reduziblen Integralen angehört, auch $M^{\prime }$ ein Element einer $(p-q)$fach unendlichen linearen Schar von reduziblen Integralen ist. Doch dies nur nebenbei.

Ich bemerke nun, daß $H_j$ eine lineare Funktion der $y_{\kappa }$ ist, sodaß ich schreiben kann:

$H_j={\displaystyle \sum _{i=1}^{2p}}{h}_{ij}{y}_i$ $(j=1,2,\mathrm{\dots },2q),$

wo die $h_{ij}$ ganze rationale Zahlen sind. Aus den $m_{i\kappa }$ und den $h_{i\kappa }$ kann ich nun zwei Tabellen von je $2q$ Kolonnen und $2p$ Zeilen bilden. Aus beiden kann ich gewisse $q$-reihige Determinanten bilden. Ich bezeichne die der $m$ mit $D$ und die aus denselben Zeilen der $h$ gebildete mit $D^{\prime }$. Dann setze ich

$$J=\sum D{D}^{\prime }.$$

$J$ ist nun in dem folgenden Sinne eine invariante Zahl: Sie bleibt ungeändert, wenn man irgendeines der Periodensysteme $x$ oder $\omega$ durch ein äquivalentes ersetzt. Dabei heißen zwei Periodensysteme äquivalent, wenn sie sich ganzzahlig und linear durcheinander ausdrücken lassen. Man kann nun einerseits beweisen, daß

$$J={\kappa }^2,$$

andererseits aber, daß

$$J=n^2.$$

Daraus kann man folgern, daß

$$\kappa =n.$$

Das ist der erste Beweis. Der nun folgende

Zweite Beweis ist wesentlich kürzer. Er beruht auf dem Vergleich der zu $S$ und $S^{\prime }$ gehörigen Bilinearformen $F(x,y)$ und $\mathrm{\Phi }(\omega ,{\omega }^{\prime })$. Man hat nämlich einerseits

$$F(x,y)=n\mathrm{\Phi }(\omega ,{\omega }^{\prime }),$$

andererseits

$$F(x,y)=\kappa \mathrm{\Phi }(\omega ,{\omega }^{\prime }).$$

Daraus schließt man

$$\kappa =n.$$

Ich komme nun zum Zusammenhang der Reduktionstheorie mit der Theorie der Fuchsschen Funktionen.

Bekanntlich definiert jede algebraische Kurve $C$ ein System von Fuchsschen Funktionen. Nun kann man die Tatsache, daß $C$ ein Vielfaches von $C^{\prime }$ ist, auch folgendermaßen ausdrücken. Es ist immer auf mannigfache Weise möglich, der Kurve $C^{\prime }$ eine Grenzkreisgruppe $G^{\prime }$ und $C$ eine ebensolche Gruppe $G$ zuzuordnen, sodaß $G$ eine Untergruppe von $G^{\prime }$ ist. Ist im besonderen $C$ ein $n$-faches von $C^{\prime }$, dann ist $G$ eine Untergruppe vom Index $n$ von $G^{\prime }$. Man erhält daher einen Fundamentalbereich von $G$ dadurch, daß man $n$ geeignet gewählte Fundamentalbereiche von $G^{\prime }$, die durch die Operationen von $G^{\prime }$ auseinander hervorgehen, aneinander lagert. Das Polygon $P$ von $G$ erscheint dann in $n$ Polygone $P^{\prime }(\beta )$ eingeteilt, die einem Polygon $P^{\prime }$ von $G^{\prime }$ im Sinne der nichteuklidischen Geometrie kongruent sind.

Ich bezeichne die Seiten des Polygons $P^{\prime }$ mit $\gamma (\alpha )$ und die homologen Seiten von $P^{\prime }(\beta )$ mit $\gamma (\alpha ,\beta )$. Die Seiten $\gamma (\alpha ,\beta )$ liegen entweder im Innern oder auf dem Rande von $P$. Ich nehme nun an, die Seite $\gamma ({\alpha }^{\prime })$ gehe aus $\gamma (\alpha )$ vermöge einer Operation von $G^{\prime }$ hervor. Wenn nun $\gamma (\alpha ,\beta )$ auf dem Rande von $P$ liegt, dann gibt es eine weitere Seite $\gamma ({\alpha }^{\prime },{\beta }^{\prime })$ auf diesem Rande, die mit $\gamma (\alpha ,\beta )$ vermöge einer Operation von $G$ konjugiert ist. Wenn jedoch $\gamma (\alpha ,\beta )$ im Innern von $P$ liegt, so existiert eine derartige von $\gamma (\alpha ,\beta )$ verschiedene Seite nicht, sondern es fallen $\gamma (\alpha ,\beta )$ und $\gamma ({\alpha }^{\prime },{\beta }^{\prime })$ zusammen und bilden die gemeinsame Seite von $P^{\prime }(\beta )$ und $P^{\prime }({\beta }^{\prime })$. Aber wie dem auch sei, jedenfalls entspricht jeder Seite $\gamma (\alpha )$ von $P^{\prime }$ eine Permutation der $n$ Ziffern $1$, $2$, $\mathrm{\dots }$, $n$.

Eine der eben durchgeführten ganz ähnliche Betrachtung können wir auch für die Ecken von $P^{\prime }$ anstellen. So wie wir nämlich die Seiten in Paare zusammenfaßten, so können wir die Ecken in Zyklen einteilen, so daß die Ecken eines Zyklus auseinander durch die Operationen von $G^{\prime }$ hervorgehen. Jedem solchen Zyklus kann wieder eine bestimmte Vertauschung der $n$ Ziffern $1$, $2$, $\mathrm{\dots }$, $n$ zugeordnet werden, die sich aus den den Seiten zugeordneten gewinnen läßt. Ich nehme nun an, es habe $P$ $2N$ Seiten und $Q$ Eckenzyklen. $2N^{\prime }$ und $Q^{\prime }$ sollen die gleiche Bedeutung für $P^{\prime }$ haben. Die einem Eckenzyklus von $P^{\prime }$ entsprechende Permutation läßt sich in zyklische Permutationen zerlegen. Bei allen Eckenzyklen mögen dabei im ganzen ${\lambda }_i$ zyklische Permutationen von gerade $i$ Ziffern vorkommen. Dann bestehen die folgenden Relationen:

$2p$ $=N-Q+1,$

$2q$ $=N^{\prime }-Q^{\prime }+1,$

$Q+2p-2$ $=n(Q^{\prime }+2q-2),$

$n(Q^{\prime }-Q)$ $=2(p-1)-2n(q-1),$

${\displaystyle \sum {\lambda }_i}$ $=Q,$

${\displaystyle \sum i{\lambda }_i}$ $=n{Q}^{\prime }.$

Die bisher gegebenen allgemeinen Betrachtungen setzen uns nun instand, eine Reihe schöner und wichtiger Sätze über die nichteuklidische Geometrie der Kreisbogenpolygone, sowie über die Geometrie der algebraischen Kurven abzuleiten. Ich will im folgenden einige Beispiele solcher Sätze anführen, ohne mich des näheren auf Beweise einzulassen, deren Grundzüge übrigens im vorstehenden enthalten sind.

1) $p=3$, $q=2$, $n=2$, $m=m^{\prime }=4$.

Mit $m$ und $m^{\prime }$ sind dabei die Ordnungen der Kurven $C$ und $C^{\prime }$ bezeichnet. $C$ hat keinen Doppelpunkt, $C^{\prime }$ hat einen Doppelpunkt. Von den 28 Doppeltangenten von $C$ gehen sechs durch einen Punkt außerhalb der Kurve.

2) $p=4$, $q=2$, $n=2$, $m=4$, $m^{\prime }=5$.

$C$ hat zwei Doppelpunkte, $C^{\prime }$ nur einen. Setzt man die Differentiale der reduziblen Integrale erster Gattung gleich Null, so erhält man ein Kegelschnittbüschel, dessen vier Basispunkte von den beiden Doppelpunkten von $C$ und zwei weiteren Punkten derselben Kurve gebildet werden. Sechs dieser Kegelschnitte berühren $C$ doppelt. Derjenige derselben, der $C$ in einem Basispunkte berührt, oskuliert daselbst.

3) $p=2$, $q=1$, $n=2$.

Die Kurve $C$ ist ein Vielfaches von zwei verschiedenen Kurven $C^{\prime }$ und $C^{\prime \prime }$. Es existiert eine Fuchssche Gruppe $G$, zu der man sowohl ein erstes Polygon $P_1$ konstruieren kann, das aus zwei Polygonen einer zu $C^{\prime }$ gehörigen Gruppe $G^{\prime }$ besteht, als auch ein zweites Polygon $P_2$, das aus zwei Polygonen einer zu $C^{\prime \prime }$ gehörigen Gruppe $G^{\prime \prime }$ besteht. $G$ ist also sowohl in $G^{\prime }$ als in $G^{\prime \prime }$ als Untergruppe vom Index $2$ enthalten. Die nebenstehende schematische Figur möge zur Veranschaulichung der Verhältnisse dienen. Die beiden eben erwähnten Fundamentalbereiche $P_1$ und $P_2$ von $G$ sind durch die Polygone mit den Ecken $A$ bzw. $C$ dargestellt. Jedes derselben zerfällt in zwei Sechsecke, die bzw. Fundamentalbereiche von $G^{\prime }$ oder $G^{\prime \prime }$ sind. Um die Äquivalenz von $P_1$ und $P_2$ besser hervortreten zu lassen, sind die Symmetriezentren der erwähnten Sechsecke mit den Seitenmitten verbunden, sodaß alle Polygone sich in leicht ersichtlicher Weise aus den so entstehenden Vierecken aufbauen.

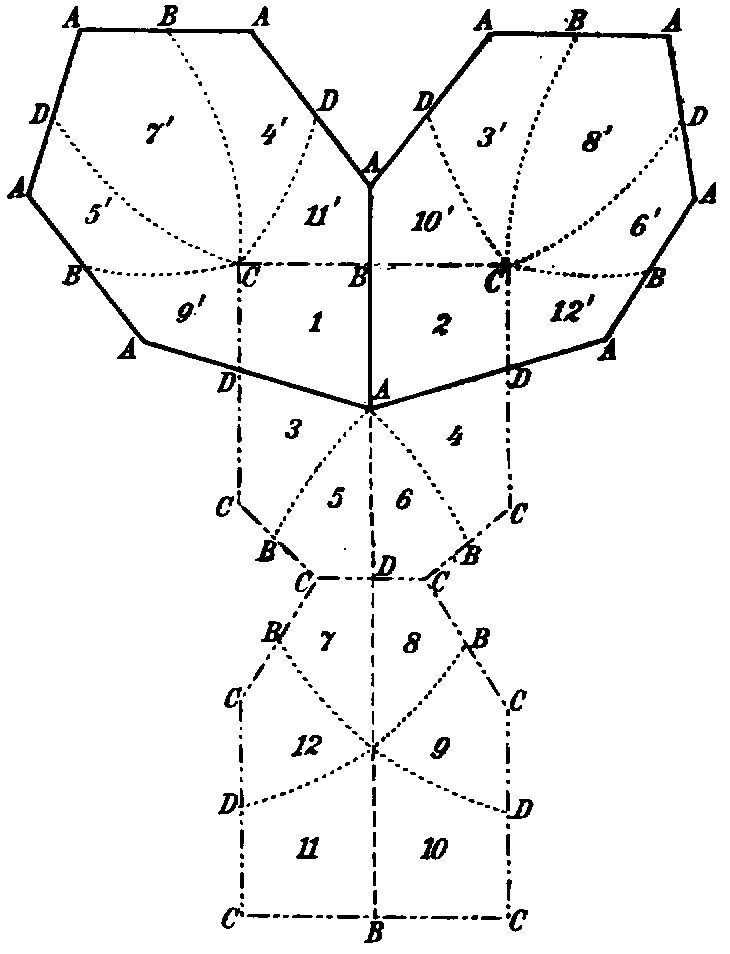
Ich gehe nun zu den Sätzen aus der Geometrie der algebraischen Kurven über, die uns dieses Beispiel lehrt. Wenn ich auf $C^{\prime }$ einen Punkt $M^{\prime }$ markiere, so entsprechen diesem zwei Punkte $M_a$ und $M_b$ auf $C$. Jedem von diesen entspricht ein Punkt von $C^{\prime \prime }$: $M_a^{\prime \prime }$, $M_b^{\prime \prime }$. Es entsprechen also im allgemeinen jedem Punkte von $C^{\prime }$ zwei Punkte von $C^{\prime \prime }$. Ebenso kann man schließen, daß im allgemeinen jedem Punkte von $C^{\prime \prime }$ zwei Punkte von $C^{\prime }$ entsprechen. Die Korrespondenz $(C^{\prime },C)$ hat aber zwei Verzweigungspunkte $M_1{}^{\prime }$, $M_2{}^{\prime }$. Jedem von ihnen entspricht also nur ein Punkt von $C$ und also auch nur ein Punkt von $C^{\prime \prime }$: $M_1^{\prime \prime }$, $M_2^{\prime \prime }$. Ebenso hat die Korrespondenz $(C^{\prime \prime },C)$ zwei Verzweigungspunkte $N_1^{\prime \prime }$, $N_2^{\prime \prime }$. Jedem von ihnen ist nur ein Punkt von $C^{\prime }$ zugeordnet: $N_1{}^{\prime }$, $N_2{}^{\prime }$. Wir können dann den ersten Satz, den wir anführen wollen, so aussprechen:

$N_1{}^{\prime }$ und $N_{\mathrm{2}}{}^{\mathrm{\prime }}$ einerseits und $M_{\mathrm{1}}^{\mathrm{\prime \prime }}$ und $M_{\mathrm{2}}^{\mathrm{\prime \prime }}$ andererseits fallen zusammen.

Ich gehe zum zweiten Satz über, der sich ergibt, wenn man $C^{\prime }$ und $C^{\prime \prime }$ als Kurven dritter Ordnung voraussetzt.

Ich kann in $N_{\mathrm{1}}{}^{\mathrm{\prime }}\mathrm{=}N_{\mathrm{2}}{}^{\mathrm{\prime }}$ die Tangente an $C^{\mathrm{\prime }}$ ziehen. Ich verbinde ferner $M_{\mathrm{1}}{}^{\mathrm{\prime }}$ und $M_{\mathrm{2}}{}^{\mathrm{\prime }}$ durch eine Sekante. Diese beiden Geraden schneiden sich auf $C^{\mathrm{\prime }}$. Ebenso kann ich in $M_{\mathrm{1}}^{\mathrm{\prime \prime }}\mathrm{=}{M}_{\mathrm{2}}^{\mathrm{\prime \prime }}$ die Tangente an $C^{\mathrm{\prime \prime }}$ ziehen und mit der Sekante $N_{\mathrm{1}}^{\mathrm{\prime \prime }}\mathit{}{N}_{\mathrm{2}}^{\mathrm{\prime \prime }}$ zum Schnitt bringen. Der Schnittpunkt liegt auf $C^{\mathrm{\prime \prime }}$.

Diese wenigen Beispiele lassen zur Genüge erkennen, wie zahlreich die besonderen Fälle sind.