La mécanique nouvelle

Si quelque partie de la science paraissait solidement établie, c’était certainement la mécanique newtonienne ; on s’appuyait sur elle avec confiance et il ne semblait pas qu’elle pût jamais être ébranlée. Mais les théories scientifiques sont comme les empires, et si Bossuet était ici, il trouverait sans doute des accents éloquents pour en dénoncer la fragilité. Toujours est-il que la Mécanique newtonienne commence à rencontrer des sceptiques, et qu’on nous annonce déjà que son temps est fini. Je voudrais vous faire connaître quelles sont les raisons de ces hérétiques et il faut avouer que quelques-unes d’entre elles ne sont pas sans valeur ; et je voudrais surtout vous expliquer en quoi consiste la mécanique nouvelle qu’on se propose de mettre à la place de l’ancienne.

Le principe fondamental de la dynamique de Newton, c’était celui qui nous enseigne que les effets d’une force sur un corps mobile sont indépendants de la vitesse antérieurement acquise par ce mobile. Un corps part du repos, une force agit sur lui pendant une seconde, et elle lui communique une vitesse v ; si on fait agir la même force pendant une deuxième seconde, elle communiquera au corps un nouvel accroissement dé vitesse égal au premier, c’est-à-dire à v et la vitesse deviendra 2v ; si elle agit encore pendant une troisième seconde, la vitesse deviendra 3v, et ainsi de suite. De sorte qu’en continuant l’action de cette même force pendant des temps suffisamment longs, on pourra obtenir des vitesses aussi grandes que l’on voudra.

Eh bien, c’est précisément ce principe qui est révoqué en doute. On dit maintenant que si la force agit pendant une deuxième seconde, son effet sera moindre que celui qu’elle a produit pendant la première ; qu’il sera moindre encore pendant la troisième seconde, et en général qu’il sera d’autant plus petit que la vitesse déjà acquise par le corps sera plus grande. Et comme ces accroissements successifs de la vitesse sont de plus en plus petits, comme la vitesse augmente de plus en plus lentement, il y aura une limite qu’elle ne pourra jamais dépasser, quelque longtemps que l’on prolonge l’action de la force accélératrice et cette limite, c’est la vitesse de la lumière. L’inertie de la matière paraît ainsi d’autant plus grande que cette matière est animée d’un mouvement plus rapide ; en d’autres termes, la masse d’un corps matériel n’est plus constante, elle augmente avec la vitesse de ce corps.

Et ce n’est pas tout ; une force peut agir dans le sens de la vitesse du mobile, ou perpendiculairement à cette vitesse. Dans le premier cas, elle tend à accélérer le mouvement, ou au contraire à le ralentir si elle est de sens contraire à ce mouvement ; mais la trajectoire reste rectiligne. Dans le second cas, elle tend à dévier le mobile de son chemin et par conséquent à courber sa trajectoire. D’après l’ancienne mécanique, l’accélération produite par une même force sur un même corps serait la même dans les deux cas. Cela ne serait plus vrai, d’après les idées nouvelles qu’on cherche à faire, prévaloir. Un corps mobile, par suite de son inertie, opposerait une résistance soit à la cause qui tend à accélérer son mouvement, soit à celle qui tend à en changer la direction ; mais si la vitesse est grande, cette résistance ne serait pas la même dans les deux cas.

Comment peut-on le savoir ? une expérience directe est-elle possible ? Il est clair que s’il y a une divergence, elle ne peut être sensible que pour des vitesses tout à fait énormes ; sans quoi cette divergence aurait été remarquée depuis longtemps parles expérimentateurs. Or, sous le rapport de la vitesse, on a fait depuis quelque temps des progrès considérables. Vous croyez peut-être que je veux faire allusion aux merveilles de l’automobilisme ; eh bien, pas du tout ; les automobiles font quelquefois du 100 à l’heure mais, au point de vue qui nous occupe, c’est une vraie vitesse d’escargot. Depuis longtemps nous avons mieux que cela, nous avons les corps célestes ; le plus rapide d’entre eux est Mercure, il fait aussi du 100, non pas à l’heure, mais à la seconde. Malheureusement c’est encore insuffisant. Je ne parle pas non plus de nos pauvres boulets de canon qui ne font pas même un kilomètre par seconde.

Seulement, depuis quelque temps, nous avons une artillerie dont les projectiles sont beaucoup plus rapides. Je veux parler du radium, on a découvert que les effets étonnants de ce corps sont dus à ce qu’il émet dans tous les sens des particules extraordinairement

[171]

ténues qui constituent un véritable bombardement. Si nous comparons cette artillerie à celle des armées européennes, nous voyons que la rapidité du tir est beaucoup plus grande ainsi que la vitesse initiale des obus ; malheureusement le calibre est beaucoup trop petit et c’est pourquoi aucune puissance ne songe à l’adopter.

Cette vitesse initiale est le dixième ou le tiers de celle de la lumière : 30.000 ou 100.000 kilomètres par seconde ; elle laisse donc loin derrière elle celle des planètes les plus rapides et elle commence à être assez grande pour que les divergences entre la mécanique ancienne et la mécanique nouvelle puissent être mises en évidence.

Comment peut-on maintenant expérimenter sur des projectiles aussi rapides. Il me faut d’abord rappeler que le radium émet trois sortes de rayons, appelés $\alpha$, $\beta$ et $\gamma$ ; les rayons $\alpha$ sont beaucoup trop lents pour notre objet ; les rayons $\gamma$ analogues aux rayons X ne peuvent pas non plus convenir. Il faut s’adresser aux rayons $\beta$ analogues aux rayons cathodiques. Les projectiles correspondants en effet sont chargés, non pas de mélinite comme nos obus, mais d’électricité ; cela est hors de doute, puisqu’en soumettant un cylindre de Faraday pendant un certain temps à ce bombardement, on constate qu’il s’électrise. Qu’en résulte-t-il ? Si ces rayons traversent un champ électrique, ce champ agira sur leur charge et déviera le rayon ; la trajectoire sera d’autant plus tendue que la force vive du projectile sera plus grande, c’est-à-dire, d’une part, qu’il sera plus gros, ou plutôt que son inertie sera plus grande, et d’autre part, qu’il sera plus rapide. Elle sera, au contraire, d’autant moins tendue que la force déviante sera plus grande, c’est-à-dire que leur charge électrique sera plus grande. C’est tout à l’ait analogue à qui se passe, pour notre artillerie. Supposons maintenant que nos rayons traversent un champ magnétique ; on sait que le champ magnétique agit sur les courants. Or un rayon $\beta$, c’est un courant puisque c’est un transport d’électricité. La force déviante, qui sera proportionnelle à ce courant, sera donc, d’une part, d’autant plus grande que la charge sera plus grande, ainsi qu’il arrivait tout à l’heure dans le cas du champ électrique ; mais, de plus, elle sera d’autant plus grande que la vitesse du projectile et, par conséquent, la vitesse de cette charge électrique sera elle-même plus grande.

On conçoit donc, sans qu’il soit nécessaire de faire de calcul, que la comparaison de ces deux déviations nous fera connaître deux choses, la vitesse d’une part, et, d’autre part, le rapport de l’inertie à la charge. Les expériences les plus récentes sont celles de M. Bucherer. Quel a été le résultat de ces expériences ? Nous avons des raisons d’admettre que tous les projectiles sont identiques et ont même charge, et qu’ils ne diffèrent que par leur vitesse. Alors, si leur inertie ne dépendait pas de leur vitesse, on trouverait que le rapport de la charge à l’inertie est constant ; c’est le résultat auquel conduirait l’ancienne mécanique ;, ce n’est pas celui auquel conduisent les expériences de MM. Kaufmam et Bucherer ; il y a une relation entre la vitesse des diverses sortes de rayons $\beta$ et le rapport de l’inertie à la charge, et cette relation nous montre que l’inertie croît avec la vitesse, ce qui est conforme aux principes de la mécanique nouvelle.

Voilà donc une des preuves invoquées par les novateurs à l’appui de leurs idées. Il y a un autre ordre de preuves, empruntées à des considérations tout à fait différentes. Vous savez en quoi consiste le principe de relativité.

Je suppose un observateur qui se déplace vers la droite ; tout se passe pour lui comme s’il était au repos, les objets qui l’entourent se déplaçant vers la gauche : aucun moyen ne permet de savoir si les objets se déplacent réellement, si l’observateur est immobile ou en mouvement. On l’enseigne dans tous les cours de mécanique, le passager sur le bateau croit voir le rivage du fleuve se déplacer, tandis qu’il est doucement entraîné par le mouvement du navire. Examinée de plus près, cette simple notion acquiert une importance capitale ; on n’a aucun moyen de trancher la question, aucune expérience ne peut mettre en défaut le principe : il n’y a pas d’espace absolu, tous les déplacements que nous pouvons observer sont des déplacements relatifs. Ces considérations, bien familières aux philosophes, j’ai eu quelquefois l’occasion de les exprimer ; j’en ai même recueilli une publicité dont je me serais volontiers passé ; tous les journaux réactionnaires français m’ont fait démontrer que le soleil tourne autour de la terre ; dans le fameux procès entre l’Inquisition et Galilée, Galilée aurait eu tous les torts.

Il est à peine nécessaire de dire ici que je n’ai jamais eu une telle pensée ; c’est bien pour la vérité que Galilée combattait, puisque, sans lui, l’Astronomie et la Mécanique céleste n’auraient pu se développer. Mais ce n’est pas de cela qu’il s’agit pour le moment.

Revenons à l’ancienne mécanique ; elle admettait le principe de relativité, et même on démontrait dans les cours les lois de cette mécanique en les déduisant de ce principe fondamental. Ces considérations suffisaient pour les phénomènes purement mécaniques, mais cela n’allait plus pour d’importantes parties de la physique, l’optique par exemple. On considérait comme absolue la vitesse de la lumière relativement à l’éther ; cette vitesse pouvait être mesurée, on avait théoriquement le moyen de comparer le déplacement d’un mobile à un déplacement

[172]

absolu, le moyen de décider si oui ou non un corps était en mouvement absolu. Vous connaissez le phénomène de l’aberration des étoiles fixes en vertu duquel les étoiles sont vues, non pas dans la direction de la vitesse absolue du rayon lumineux qu’elles nous envoient, mais dans celle de la vitesse relative de ce rayon par rapport à la Terre. Je représente en OA (fig. 26) la vitesse absolue de la lumière émanée

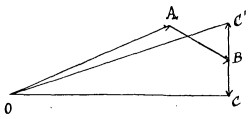
Figure 26.

de l’étoile ; en AB la vitesse du Soleil dans l’espace, changée de sens ; en BC la vitesse de la Terre par rapport au Soleil, changée de sens. Alors OC sera la vitesse relative de la Lumière, et l’étoile, qui devait être vue dans la direction OA, sera vue dans la direction OC. Au bout de 6 mois, la vitesse BC aura changé de sens et sera devenue BC, et l’étoile sera vue dans la direction OC’ ; cette variation de direction de OC à OC’ nous renseigne donc sur la vitesse BC’ ; ce qui n’a rien de contraire au principe, puisqu’il s’agit ici d’une vitesse relative.

Mais regardons la chose d’un peu plus près. Soient deux étoiles diamétralement opposées sur la sphère céleste, dans la direction du mouvement du Soleil dans l’espace (fig.27). Les vitesses absolues des rayons

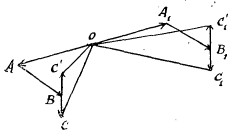
Figure 27.

lumineux partant de ces deux étoiles sont représentées par les deux droites $OA$ et $O{A}_1$, égales et opposées. D’autre part $AB=A_1{B}_1$, $BC=B_1{C}_1=B{C}^{\prime }=B_1^{\prime }{C}_1^{\prime }$. La direction apparente de l’une des étoiles varie entre $OC$ et $O{C}^{\prime }$, l’autre entre $OC$, et $O{C}_1^{\prime }$. Mais on voit que l’angle $CO{C}^{\prime }$ est plus petit que l’angle $C_1^{\prime }O{C}_1^{\prime }$, de sorte que l’une des étoiles exécute des oscillations apparentes de plus grande amplitude ; et la comparaison de ces amplitudes devrait nous renseigner sur la vitesse $AB$ qui est une vitesse absolue, et cela serait contraire au principe de relativité. Nous verrons bientôt comment la Nouvelle Mécanique se tire de cette difficulté.

Des expériences délicates, faites avec des appareils extrêmement précis, que je ne décrirai pas devant vous, ont permis d’essayer la réalisation pratique d’une pareille comparaison : le résultat a été nul. Le principe de relativité n’admet aucune restriction dans la nouvelle mécanique ; il a, si j’ose ainsi dire, une valeur absolue.

Comment de pareilles expériences étaient-elles possibles ? Supposons un appareil optique quelconque ; il est entraîné dans le mouvement de la Terre, qui se compose de deux parties, la vitesse de la Terre sur son orbite qui est connue et la vitesse absolue du Soleil dans l’espace qui est inconnue. Au bout de 12 heures, l’appareil entraîné par la rotation de la Terre se trouve avoir changé d’orientation ; et comme il n’est plus orienté de la même façon par rapport à cette translation dans laquelle il est entraîné, les phénomènes optiques dont il est le siège devraient être modifiés si cette vitesse de translation avait une influence quelconque. Or, on constate qu’ils ne sont pas modifiés, bien que les appareils soient assez sensibles pour mettre en évidence la plus légère modification.

Et le résultat est tellement général que, pour en revenir à notre figure de tout à l’heure à propos de l’aberration avec nos deux couples, $CO{C}^{\prime }$, $C_{1}O{C}_1^{\prime }$, je suis absolument sûr d’avance que l’on ne trouvera aucune différence entre les amplitudes des oscillations annuelles des différentes étoiles et qu’on n’aura par conséquent aucun moyen de connaître la vitesse absolue du Soleil. Et cela, bien que les procédés astronomiques dont nous disposons actuellement soient assez précis pour qu’on puisse faire l’observation directement.

Quel rôle joue le principe de relativité dans la Nouvelle Mécanique ? Nous sommes d’abord amenés à parler du temps apparent, une invention fort ingénieuse du physicien Lorentz. Nous supposons deux observateurs, l’un A à Paris, l’autre B à Berlin. A et B ont des chronomètres identiques et veulent les régler ; mais ce sont des observateurs méticuleux comme il n’y en a guère ; ils exigent dans leur réglage une extraordinaire exactitude ; ce sera, par exemple, non une seconde, mais un milliardième de seconde. Comment pourront-ils faire ? De Paris à Berlin, A envoie un signal télégraphique, avec un sans-fil, si vous voulez, pour être tout à fait moderne. B note le moment de la réception et ce sera pour les deux chronomètres l’origine du temps. Mais le signal emploie un certain temps pour aller de Paris à Berlin ; il ne va qu’avec la vitesse de la lumière ; la montre de B serait donc en retard ; B est trop intelligent

[173]

pour ne point s’en rendre compte ; il va remédier à cet inconvénient. La chose semble bien simple : on croise les signaux, A reçoit et B envoie, on prend la moyenne des corrections ainsi faites, on a l’heure exacte. Mais cela est-il bien certain ? Nous supposons que, de $A$ à $B$, le signal emploie le même temps que pour aller de B à A. Or A et B sont emportés dans le mouvement de la terre par rapport à l’éther, véhicule des ondes électriques. Quand A a envoyé son signal, il fuit devant lui, B s’éloigne de même, le temps employé sera plus long que si les deux observateurs étaient au repos. Si, au contraire, c’est B qui envoie, A qui reçoit, le temps est plus court parce que A va au devant des signaux ; il leur est absolument impossible de savoir si leurs chronomètres marquent ou non la même heure.

Quelle que soit la méthode employée, les inconvénients restent les mêmes ; l’observation d’un phénomène astronomique, une méthode optique quelconque se heurtent aux mêmes difficultés ; B ne pourra jamais connaître qu’une différence apparente de temps, qu’une espèce d’heure locale. Le principe de relativité s’applique intégralement.

Dans l’ancienne mécanique pourtant, on démontrait avec ce principe toutes les lois fondamentales. On pourrait être tenté de reprendre les raisonnements classiques et de raisonner comme il suit : Soit encore deux observateurs, A et B, pour les nommer comme on nomme toujours deux observateurs en mathématiques ; supposons-les en mouvement, s’éloignant l’un de l’autre ; aucun d’eux ne peut dépasser la vitesse de la lumière ; par exemple, B sera animé d’une vitesse de 200.000 kilomètres vers la droite, A de 200.000 vers la gauche. A peut se croire au repos et la vitesse apparente de B sera, pour lui, 400.000 kilomètres. Ou bien, au contraire, A peut croire que B est au repos, et que c’est lui A qui se déplace avec une vitesse de 400.000 kilomètres. Si A connaît la mécanique nouvelle, il se dira: B a une vitesse qu’il ne peut atteindre. C’est donc que, moi aussi, je suis en mouvement. Ou même, sans savoir la nouvelle mécanique, il pourrait dire : mais si je m’éloignais de B avec une vitesse supérieure à celle de la lumière, les rayons émanés de B ne pourraient m’atteindre, je ne pourrais le voir ; or, je le vois, donc B n’est pas en repos. Il semble donc qu’il pourrait décider de sa situation absolue. Mais il faudrait qu’il puisse observer le mouvement de B lui-même. Or, comment les choses se passent-elles avec la mécanique nouvelle ?

Pour faire cette observation, A et B commencent par régler leurs montres, puis B envoie à A des télégrammes pour lui indiquer ses positions successives ; en les réunissant, A peut se rendre compte du mouvement de B et tracer la courbe de ce mouvement. Or les signaux se propagent avec la vitesse de la lumière ; les montres qui marquent le temps apparent varient à chaque instant et tout se passera comme si la montre de B avançait. B croira aller beaucoup moins vite et la vitesse apparente qu’il aura relativement à A ne dépassera pas la limite qu’elle ne doit pas atteindre. Rien ne pourra révéler à A s’il est en mouvement ou en repos absolu.

Il faut encore faire une autre hypothèse beaucoup plus surprenante, beaucoup plus difficile à admettre, qui gêne beaucoup nos habitudes actuelles. Un corps, en mouvement de translation, subit une déformation dans le sens même où il se déplace ; une sphère, par exemple, devient comme une espèce d’ellipsoïde aplati dont le petit axe serait parallèle à la translation. Si l’on ne s’aperçoit pas tous les jours d’une transformation pareille, c’est qu’elle est d’une petitesse qui la rend presque imperceptible. La Terre, emportée dans sa révolution sur son orbite, se déforme environ de 1/200.000.000 : pour observer un pareil phénomène, il faudrait donc des instruments de mesure d’une précision extrême ; mais, leur précision serait-elle infinie qu’on n’en serait pas plus avancé, car, emportés eux aussi dans le mouvement, ils subissent la même déformation. On ne s’apercevra de rien ; le mètre que l’on pourrait employer deviendra plus court, comme la longueur qu’on mesure. On ne peut savoir quelque chose qu’en comparant, à la vitesse de la lumière, la longueur de l’un de ces corps.

Ce sont là de délicates expériences, réalisées par Michelson, et dont je ne vous exposerai pas le détail ; elles ont donné des résultats tout à fait remarquables ; quelque étranges qu’ils nous paraissent, il faut admettre que la troisième hypothèse est parfaitement vérifiée.

Pour nous rendre compte des conséquences de cette hypothèse, imaginons un corps lumineux animé d’un mouvement de translation ; les ondes successives, émanées de ce corps, auront une forme sphérique ; les rayons de ces sphères seront d’autant plus grands que l’onde aura été émise il y a plus longtemps et qu’elle aura en conséquence parcouru plus de chemin ; le centre de chaque sphère sera au point qu’occupait le corps lumineux au moment de l’émission.

Toutes ces sphères sont donc homothétiques entre elles et leur centre commun d’homothétie est la position actuelle du corps lumineux.

Supposons maintenant un observateur entraîné dans la même translation que le corps lumineux. Ce corps lumineux lui paraîtra fixe ; mais ce n’est pas tout. Comme il se trouve, ainsi que nous venons de le dire, aplati dans le sens du mouvement, et qu’il en est de même de tous les objets qui l’entourent, et qui sont entraînés avec lui dans une translation commune, il n’a aucun moyen de s’apercevoir de cet

[174]

aplatissement, qui est commun aux corps à mesurer et aux instruments de mesure. Si, par hasard, un objet échappait à cette déformation, c’est cet objet qui lui paraîtrait non pas aplati, mais au contraire allongé dans la direction de la translation. Or, un pareil objet existe, ce sont les surfaces d’onde qui ne sont pas déformées et qui demeurent sphériques. Ces surfaces d’onde sembleront donc à notre observateur allongées dans le sens du mouvement ; elles lui paraîtront ellipsoïdales. Tous ces ellipsoïdes seront homothétiques entre eux, et le corps lumineux en occupera un foyer.

Dans ces conditions, un théorème de géométrie très simple montre que le temps apparent que la lumière mettra à aller de $A$ en $B$, c’est-à-dire la différence entre le temps local en $A$ au moment du départ de $A$, et le temps local en $B$ au moment de l’arrivée en $B$, que ce temps apparent, dis-je, est le même que si la translation n’existait pas, ce qui est bien conforme au principe de relativité.

Et maintenant, nous sommes en mesure de répondre à une question posée plus haut. Je reprends la figure que je faisais tout à l’heure à propos de l’aberration des étoiles. Nous avons vu que l’angle $CO{C}^{\prime }$, (fig. 27) qui mesure l’amplitude de l’oscillation annuelle d’une étoile produite par l’aberration, n’est pas égal à l’angle $C_{1}O{C}_1^{\prime }$, qui mesure l’amplitude de celle de l’étoile diamétralement opposée. Nous avons dit que la comparaison de ces deux angles pourrait nous révéler la vitesse absolue du Soleil, ce qui est contraire au principe de relativité.

Puisque nous admettons maintenant ce principe, il faut bien qu’on n’ait aucun moyen de reconnaître que ces deux angles sont différents, et cela semble d’abord un peu mystérieux. Mais nos instruments de mesure, c’est-à-dire les cercles gradués dont se servent les astronomes, sont déformés par la translation du Soleil, ainsi que je l’expliquais à l’instant ; naturellement cette déformation altère nos mesures ; et elle les altère précisément de façon à réaliser une parfaite compensation. Telle serait, d’après les partisans de la Nouvelle Mécanique, l’explication de ce fait paradoxal.

Telles sont les bases de la nouvelle mécanique ; avec l’appui de ces hypothèses, on trouve qu’elle est compatible avec le principe de relativité.

Mais il faut la rattacher alors à une conception nouvelle de la matière.

Pour le physicien moderne, l’atome n’est plus l’élément simple ; il est devenu un véritable univers dans lequel des milliers de planètes gravitent autour de soleils minuscules. Soleils et planètes sont ici des particules électrisées, soit négativement, soit positivement ; le physicien les appelle électrons et bâtit le monde avec elles. D’aucuns se représentent l’atome neutre comme une masse centrale positive autour de laquelle circulent un grand nombre d’électrons chargés négativement, dont la masse électrique totale est égale en grandeur à celle du noyau central.

Cette conception de la matière permet de rendre compte aisément de l’augmentation de la masse d’un corps avec sa vitesse, dont nous avons fait un des caractères de la mécanique nouvelle. Un corps quelconque n’étant qu’un assemblage d’électrons, il nous suffira de le montrer sur ces derniers. Remarquons, à cet effet, qu’un électron isolé se déplaçant à travers l’éther engendre un courant électrique, c’est-à-dire un champ électro-magnétique. Ce champ correspond à une certaine quantité d’énergie localisée, non dans l’électron, mais dans l’éther. Une variation, en grandeur ou en direction, de la vitesse de l’électron modifie le champ et se traduit par une variation de l’énergie électromagnétique de l’éther. Alors que, dans la mécanique newtonienne, la dépense d’énergie n’est due qu’à l’inertie du corps en mouvement, ici une partie de cette dépense est due à ce qu’on peut appeler l’inertie de l’éther relativement aux forces électromagnétiques. Cette inertie de l’éther est un phénomène bien connu ; c’est ce que les électriciens appelle la self-induction. Un courant dans un fil a de la peine à s’établir, de même qu’un mobile en repos a de la peine à se mettre en mouvement, c’est une véritable inertie. En revanche, un courant, une fois établi, tend à se maintenir, de même qu’un mobile une fois lancé ne s’arrête pas tout seul ; et, c’est pourquoi vous voyez jaillir des étincelles quand le trolley quitte un instant le fil qui amène le courant. L’inertie de l’éther augmente avec la vitesse et sa limite devient infinie lorsque la vitesse tend vers la vitesse de la lumière. La masse apparente de l’électron augmente donc avec la vitesse ; les expériences de Kaufmann montrent que la masse réelle constante de l’électron est négligeable par rapport à la masse apparente ; elle peut être considérée comme nulle, de sorte que si c’est la masse qui constitue la matière, on pourrait presque dire qu’il n’y a plus de matière.

Dans cette nouvelle conception, la masse constante de la matière a disparu. L’éther seul, et non plus la matière, est inerte. Seul, l’éther oppose une résistance au mouvement, si bien que l’on pourrait dire : il n’y a pas de matière, il n’y a que des trous dans l’éther. Pour les mouvements stationnaires ou quasi-stationnaires, la mécanique nouvelle ne diffère pas, au degré d’approximation de nos mesures près, de la mécanique newtonienne, avec cette différence toutefois que la masse dépend de la vitesse et de l’angle de cette vitesse avec la direction de la force accélératrice. Si, par contre, la vitesse a une accélération

[175]

considérable, dans le cas, par exemple, d’oscillations très rapides, il y a production d’ondes hertziennes représentant, une perte de l’énergie de l’électron entraînant l’amortissement de son mouvement. Ainsi, dans la télégraphie sans fil, les ondes émises sont dues aux oscillations des électrons dans la décharge oscillante. Et cela, arrivera toutes les fois qu’il y aura un changement brusque de vitesse, soit en grandeur, soit en direction.

Des vibrations analogues ont lieu, dans une flamme, ou encore dans un corps incandescent. Pour Lorentz, il circule à l’intérieur d’un corps incandescent un nombre considérable d’électrons qui, ne pouvant pas en sortir, volent dans tous les sens et se réfléchissent sur sa surface. On pourrait les comparer à une nuée de moucherons enfermés dans un bocal et venant frapper de leurs ailes les parois de leur prison. Plus la température est élevée, plus le mouvement de ces électrons est rapide et plus les chocs mutuels et les réflexions sur la paroi sont nombreuses. A chaque choc, à chaque réflexion, une onde électromagnétique est émise, car chacune de ces réflexions est un changement brusque de vitesse, et c’est la perception de ces ondes qui nous fait paraître le corps incandescent.

Le mouvement des électrons est presque tangible dans un tube de Crookes. Il s’y produit un véritable bombardement d’électrons partant de la cathode. Ces rayons cathodiques frappent violemment l’anticathode et s’y réfléchissent en partie ou y perdent leur vitesse, donnant ainsi naissance à un ébranlement électromagnétique que plusieurs physiciens identifient avec les rayons Röntgen.

Il nous reste, en terminant, à examiner les restions de la mécanique nouvelle avec l’astronomie.

La notion de masse constante d’un corps s’évanouissant, que deviendra la loi de Newton ? Elle, ne pourra subsister que pour des corps en repos. De plus, il faudra tenir compte du fait que l’attraction n’est pas instantanée.

On peut donc se demander avec raison si la mécanique nouvelle ne va réussir qu’à compliquer l’astronomie, sans obtenir une approximation supérieure à celle que nous donne la mécanique céleste classique. M. Lorentz a abordé la question.

Partant de la loi de Newton, supposée vraie pour deux corps électrisés au repos, il calcule l’action électrodynamique des courants engendrés par ces corps en mouvement ; il obtient ainsi une nouvelle loi d’attraction contenant les vitesses des deux corps comme paramètres.

La masse peut-être définie de deux manières : 1° par le quotient de la force par l’accélération ; c’est la véritable définition de la masse, qui mesure l’inertie du corps ; 2° par l’attraction qu’exerce le corps sur un corps extérieur, en vertu de la loi de Newton. Nous devons donc distinguer la masse, coefficient d’inertie, et la masse, coefficient d’attraction. D’après la loi de Newton, il y a proportionnalité rigoureuse entre ces deux coefficients. Mais cela n’est démontré que pour les vitesses auxquelles les principes généraux de la Dynamique sont applicables. Maintenant nous avons vu que la masse, coefficient d’inertie, croît avec la vitesse ; devons-nous conclure que la masse coefficient d’attraction croît également avec la vitesse et reste proportionnelle au coefficient d’inertie, ou, au contraire, que ce coefficient d’attraction demeure constant ? C’est là une question que nous n’avons aucun moyen de décider.

D’autre part, si le coefficient d’attraction dépend delà vitesse, comme les vitesses de deux corps qui s’attirent mutuellement ne sont généralement pas les mêmes, comment ce coefficient dépendra-t-il de ces deux vitesses ?

Nous ne pouvons faire à ce sujet que des hypothèses, mais nous sommes naturellement amenés à rechercher quelles seraient celles de ces hypothèses qui seraient compatibles avec le Principe de la Relativité. Il y en a un grand nombre ; la seule dont je parlerai ici est celle de Lorentz, que je vais exposer brièvement.

Considérons d’abord, des électrons en repos. Deux électrons de même signe se repoussent et deux électrons de signe contraire s’attirent ; dans la théorie ordinaire, leurs actions mutuelles sont proportionnelles à leurs charges électriques ; si donc nous avons quatre électrons, deux positifs $A$ et $A^{\prime }$, et deux négatifs $B$ et $B^{\prime }$, et que les charges de ces quatre électrons soient les mêmes, en valeur absolue, la répulsion de $A$ sur $A^{\prime }$ sera, à la même distance, égale à la répulsion de $B$ sur $B^{\prime }$ et égale encore à l’attraction de $A$ sur $B^{\prime }$ ou de $A^{\prime }$ sur $B$. Si donc $A$ et $B$ sont très près l’un de l’autre, de même que $A^{\prime }$ et $B^{\prime }$, et que nous examinions l’action du système $A^{\prime }+B^{\prime }$ sur le système. $A^{\prime }+B^{\prime }$, nous aurons deux répulsions et deux attractions qui se compenseront exactement et l’action résultante sera nulle.

Or les molécules matérielles doivent précisément être regardées comme des espèces de systèmes solaires où circulent les électrons, les uns positifs, les autres négatifs, et de telle façon que la somme algébrique de toutes les charges soit nulle. Une molécule matérielle est donc, de tout point, assimilable au système $A+B$ dont nous venons de parler, de sorte que l’action électrique totale de molécules l’une sur l’autre devrait être nulle.

Mais l’expérience nous montre que ces molécules s’attirent par suite de la gravitation newtonienne ; et alors, on peut faire deux hypothèses : on peut

[176]

supposer que la gravitation n’a aucun rapport avec les attractions électrostatiques, qu’elle est due à une cause entièrement différente, et qu’elle vient simplement s’y superposer ; ou bien, on peut admettre qu’il n’y a pas proportionnalité des attractions aux charges, et que l’attraction exercée par une charge +1 sur une charge -1 est plus grande que la répulsion mutuelle de deux charges +1 ou que celle de deux charges -1.

En d’autres termes, le champ électrique produit par les électrons positifs, et celui que produisent les électrons négatifs se superposeraient en restant distincts. Les électrons positifs seraient plus sensibles au champ produit par les électrons négatifs ; ce serait le contraire pour les électrons positifs. Il est clair que cette hypothèse complique un peu l’Electrostatique, mais qu’elle y fait rentrer la gravitation. C’était, en somme, l’hypothèse de Franklin.

Qu’arrive-t-il maintenant, si les électrons sont en mouvement ? Les électrons positifs vont engendrer une perturbation dans l’éther et y feront naître un champ électrique et un champ magnétique. Il en sera de même pour les électrons négatifs. Les électrons, tant positifs que négatifs, subiront ensuite une impulsion mécanique par l’action de ces différents champs. Dans la théorie ordinaire, le champ électromagnétique, dû au mouvement des électrons positifs, exerce, sur deux électrons de signe contraire et de même charge absolue, des actions égales et de signe contraire. On peut alors sans inconvénient ne pas distinguer le champ dû au mouvement des électrons positifs et le champ dû au mouvement des électrons négatifs, et ne considérer que la somme algébrique de ces deux champs, c’est-à-dire le champ résultant.

Dans la nouvelle théorie, au contraire, l’action sur les électrons positifs du champ électromagnétique dû aux électrons positifs se fait d’après les lois ordinaires ; il en est de même de l’action sur les électrons négatifs du champ dû aux électrons négatifs. Considérons maintenant l’action du champ dû aux électrons positifs (ou inversement) : elle suivra encore les mêmes lois, mais avec un coefficient différent. Chaque électron est plus sensible au champ créé par des électrons de nom contraire qu’au champ créé par des électrons de même nom.

Telle est l’hypothèse de Lorentz, qui se réduit à l’hypothèse de Franklin aux faibles vitesses ; elle rendra donc compte, pour ces faibles vitesses, de la loi de Newton. De plus, comme la gravitation se ramène à des forces d’origine électrodynamique, la théorie générale de Lorentz s’y appliquera, et, par conséquent, le principe de la relativité ne sera pas violé.

On voit que la loi de Newton n’est plus applicable aux grandes vitesses et qu’elle doit être modifiée, pour les corps en mouvement, précisément de la même manière que les lois de l’Electrostatique pour l’électricité en mouvement.

On sait que les perturbations électromagnétiques se propagent avec la vitesse de la lumière. On sera donc tenté de rejeter la théorie précédente, en rappelant que la gravitation se propage, d’après les calculs de Laplace, au moins dix millions de fois plus vite que la lumière, et que, par conséquent, elle ne peut être d’origine électrodynamique. Le résultat de Laplace est bien connu, mais on en ignore généralement la signification. Laplace supposait que, si la propagation de la gravitation n’est pas instantanée, sa vitesse de propagation se combine avec celle du corps attiré, comme cela se passe pour la lumière dans le phénomène de l’aberration astronomique, de telle façon que la force effective n’est pas dirigée suivant la droite qui joint les deux corps, mais fait avec cette droite un petit angle. C’est là une hypothèse toute particulière, assez mal justifiée, et, en tout cas, entièrement différente de celle de Lorentz. Le résultat de Laplace ne prouve rien contre la théorie de Lorentz.

Avant d’examiner comment cette loi rend compte des phénomènes astronomiques, remarquons encore que l’accélération des corps célestes a comme conséquence un rayonnement électromagnétique, donc une dissipation de l’énergie se faisant ressentir en retour par un amortissement de leur vitesse. J’ai dit, en effet, qu’il se produisait une radiation toutes les fois qu’un électron subissait un changement brusque de vitesse. Mais ce mot brusque manque de précision. Si le changement est lent, si l’accélération est faible il y aura encore une radiation, mais cette radiation sera très faible. Pour les corps célestes, l’accélération est quelque chose comme un milliard de fois plus petite qu’à l’anticathode d’un tube de Crookes par exemple ; la radiation sera imperceptible, elle n’en existe pas moins et elle dissipe peu à peu la force vive de la planète. A la longue les planètes finiront donc par tomber sur le Soleil. Mais cette perspective ne peut guère nous effrayer, la catastrophe ne pouvant arriver que dans quelques millions de milliards de siècles. Revenant maintenant à la loi d’attraction, nous voyons aisément que la différence entre les deux mécaniques sera d’autant plus grande que la vitesse des planètes sera plus grande. S’il y a une différence appréciable, ce sera donc pour Mercure qu’elle sera la plus grande, Mercure ayant de toutes les planètes la plus grande vitesse. Or il arrive justement que Mercure présente une anomalie non encore expliquée : le mouvement de son périhélie est plus rapide que le mouvement calculé par la théorie classique. Sa vitesse angulaire est de 38" plus

[177]

grande qu’elle ne devrait être. Le Verrier attribua cette anomalie à une planète non encore découverte et un astronome amateur crut observer son passage sur le Soleil. Depuis lors, plus personne ne l’a vue et il est malheureusement certain que cette planète aperçue n’était qu’un oiseau.

Or, la mécanique nouvelle rend bien compte du sens de l’erreur relative à Mercure, mais elle nous donne seulement un mouvement de 6" ; elle laisse donc encore une marge de 32" entre elle et l’observation. Elle ne suffit donc pas pour ramener la concordance dans la théorie de Mercure. Si ce résultat n’est guère décisif en faveur de la mécanique nouvelle, il est encore moins défavorable à son acceptation, puisque le sens dans lequel elle corrige l’écart de la théorie classique est le bon. C’est d’ailleurs, entre l’ancienne et la nouvelle mécanique, la seule différence que les observations astronomiques puissent déceler. Le périhélie est le seul élément qui soit atteint. La théorie des autres planètes n’est pas sensiblement modifiée dans la nouvelle théorie et les résultats coïncident, à l’approximation des mesures près, avec ceux de la théorie classique. Il en est encore de même en ce qui concerne la théorie de la Lune.

Pour conclure, il serait prématuré, je crois, malgré la grande valeur des arguments et des faits érigés contre elle, de regarder la mécanique classique comme définitivement condamnée. Quoi qu’il en soit, d’ailleurs, elle restera la mécanique des vitesses très petites par rapport à la vitesse de la lumière, la mécanique donc de notre vie pratique et de notre technique terrestre. Si cependant, dans quelques années sa rivale triomphe, je me permettrai de vous signaler un écueil pédagogique que n’éviteront pas nombre de maîtres, en France, tout au moins. Ces maîtres n’auront rien de plus pressé, en enseignant la mécanique élémentaire à leurs élèves, que de leur apprendre que cette mécanique-là a fait son temps, qu’une mécanique nouvelle, où les notions de masse et de temps ont une toute autre valeur, la remplace ; ils regarderont de haut cette mécanique périmée que les programmes les forcent à enseigner et feront sentir à leurs élèves le mépris qu’ils lui portent.

Je crois bien cependant que cette mécanique classique dédaignée sera aussi nécessaire que maintenant et que celui qui ne la connaîtra pas à fond ne pourra comprendre la mécanique nouvelle.

Time-stamp: "20.07.2017 00:05"