H. Poincaré to Georges-Henri Halphen

[Entre le 01.03.1881 et le 24.03.1881]

Monsieur,

Vous devez trouver que je tarde beaucoup à vous envoyer la note que je vous avais promise sur les fonctions fuchsiennes. Je vous prie de m’excuser; j’ai été presque constamment en voyage depuis que j’ai eu le plaisir de vous voir et je n’ai pas eu une minute à moi.

Voici quel a été le but de mes recherches et quelle marche j’ai suivie.

Existe-t-il des fonctions uniformes $F(z)$ telles que:

$$F(z)=F\left(\frac{{\alpha }_{1}z+{\beta }_1}{{\gamma }_{1}z+{\delta }_1}\right)=\mathrm{\cdots }=F\left(\frac{{\alpha }_{n}z+{\beta }_n}{{\gamma }_{n}z+{\delta }_n}\right).$$

Il est clair qu’en général il n’en existera pas parce que le groupe $G$ dérivé des opérations:

$$(z,\frac{{\alpha }_{1}z+{\beta }_1}{{\gamma }_{1}z+{\delta }_1}),(z,\frac{{\alpha }_{2}z+{\beta }_2}{{\gamma }_{2}z+{\delta }_2}),\mathrm{\cdots },(z,\frac{{\alpha }_{n}z+{\beta }_n}{{\gamma }_{n}z+{\delta }_n}),$$

ne sera pas discontinu, c’est à dire contiendra des opérations changeant $z$ en une quantité aussi voisine que l’on voudra de $z$ ; ou bien encore aussi voisine qu’on voudra d’une quantité donnée.

La première chose à faire est donc de rechercher les groupes conditions pour que le groupe $G$ soit discontinu.

Voici ce que je trouve à ce sujet.

Je suppose que ${\alpha }_1$, ${\beta }_1$, ${\gamma }_1$, ${\delta }_1$, ${\alpha }_2$, ${\beta }_2$, $\mathrm{\cdots }$ sont réels (Ce n’est pas là l’hypothèse que j’avais faite dans mes notes des 14 et 21 Février).

L’opération :

$$(z,\frac{{\alpha }_{1}z+{\beta }_1}{{\gamma }_{1}z+{\delta }_1})$$

sera complètement déterminée quand on saura qu’elle change $z_0$ en $t_0$ et $z_1$ en $t_1$ ; de telle sorte que :

$$t_0=\frac{{\alpha }_1{z}_0+{\beta }_1}{{\gamma }_1{z}_0+{\delta }_1},t_1=\frac{{\alpha }_1{z}_1+{\beta }_1}{{\gamma }_1{z}_1+{\delta }_1}$$

Nous l’appellerons alors l’opération $(z_0,t_0,z_1,t_1)$.

Les quatre points $z_0$, $t_0$, $z_1$, $t_1$ ne peuvent être choisis arbitrairement.

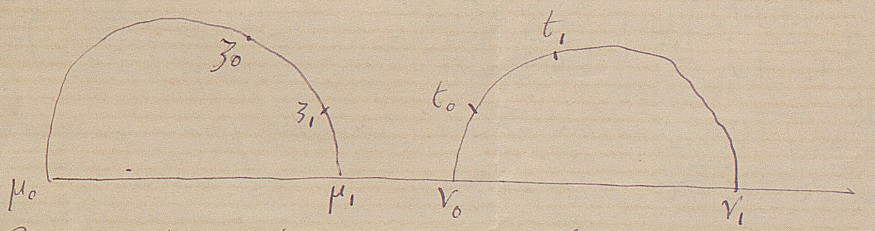
Par $z_0$ et $z_1$ et par $t_0$ et $t_1$ faisons passer deux circonférences ayant leurs centres sur l’axe des $x$ et coupant cet axe en ${\mu }_0,{\mu }_1,{\nu }_0,{\nu }_1$. On devra avoir:

$$\text{rapport anharmonique }(z_0,z_1,{\mu }_0,{\mu }_1)=\text{rapport anharmonique }(t_0,t_1,{\mu }_0,{\mu }_1).$$ (1)

Remarquons que les points $(z_0,z_1,t_0,t_1)$ peuvent être:

1° réels et en dehors de l’axe des $x$,

2° sur l’axe des $x$,

3° imaginaires.

Au lieu d’écrire in extenso la relation (1) j’écrirai pour abréger:

$$R(z_0,z_1)=R(t_0,t_1).$$

Cela posé soient $A_1$, $A_2$, $\mathrm{\cdots }$, $A_{2n}$ $2n$ points réels ou imaginaires.

Joignons $A_1$ à $A_2$ par une circonférence $B_1$ ayant son centre sur l’axe des $x$, $A_2$ à $A_3$ par une circonférence $B_2$ ayant son centre sur l’axe des $x$, etc. ; nous obtiendrons un polygone curviligne dont les éléments (sommets et côtés) se suivront dans l’ordre suivant:

$$A_1{B}_1{A}_2{B}_2{A}_3\mathrm{\cdots }{A}_{2n-1}{B}_{2n-1}{A}_{2n}{B}_{2n}{A}_1.$$

Supposons que l’on ait reparti les $2n$ côtés en paires, et cela d’une façon arbitraire; nous dirons que chaque côté est le conjugué de l’autre côté de la même paire.

Nous allons maintenant repartir les sommets en cycles de la manière suivante :

Partons d’un sommet quelconque, prenons le côté suivant, puis son conjugué, puis le sommet suivant, puis le côté suivant, puis son conjugué, etc.; on rencontrera ainsi un certain nombre de sommets et on finira par revenir au point de départ. Les sommets ainsi rencontrés formeront un cycle et tous les sommets se trouveront repartis en un certain nombre de cycles.

Conditions imposées au polygone:

1° Un même cycle ne peut contenir que des sommets réels et situés hors de l’axe des $x$; ou bien il ne peut contenir que des sommets situés sur l’axe des $x$; ou bien tous ses sommets sont imaginaires. Mais un même cycle ne peut avoir à la fois par exemple des sommets réels et imaginaires.

2° Si $B_i$ et $B_k$ sont deux côtés conjugués, on a :

$$R(A_i{A}_{i+1})=R(A_K{A}_{K+1}).$$

3° Si l’on considère un cycle dont tous les sommets sont réels, en somme des angles correspondants du polygone curviligne est une partie aliquote de 4 droits.

A ces conditions, le groupe dérivé des opérations

$$(A_i,A_{K+1};A_{i+1},A_K)$$

est discontinu et il existe une infinité de fonctions uniformes $F(z)$ qui sont inaltérées par les opérations de ce groupe.

Si cela ne vous ennuie pas trop, je vous enverrai prochainement de nouveaux détails.

Veuillez agréer, Monsieur, l’assurance de ma considération la plus distinguée,

Poincaré

ALS 4p. MS 5624.162, Bibliothèque de l’Institut de France.

Time-stamp: "29.01.2017 18:33"